El siguiente problema de Ecuación Diferencial Ejercicios Resueltos Dennis G. Zill cap 2.3. Prob 19, se desarrolla el método que proponemos para resolver cualquier ED lineal de primer orden en 4 pasos sencillos, utilízalo varias veces antes de tatar entenderlo, es mi recomendación, posteriormente podrás ver con mayor facilidad de donde salen las ecuaciones, aquí las explicaremos.
Método: Factor Integrante
1. Forma Standard: $ \frac{dy}{dx}+P\left( x \right)y=f(x)$
2. Factor Integrante: $ {{e}^{{\int }^{}P\left( x \right)dx}}$
Forma de solución: $ y={{y}_{c}}+{{y}_{p}}$
3. $ {{y}_{c}}=C{{e}^{-{\int }^{}P\left( x \right)dx}}$
4. $x {{y}_{p}}=\frac{1}{{{e}^{{\int }^{}P\left( x \right)dx}}}{\int }^{}{{e}^{{\int }^{}P\left( x \right)dx}}f(x)dx$
Ecuación Diferencial Ejercicios Resueltos Dennis G. Zill cap 2.3. Prob 19
$ (\text{x}+1)\frac{dy}{dx}+\left( x+2 \right)y=2x{{e}^{-x}}$
Pasos:
I. El primer paso consiste en escribir la forma estándar de la ED a resolver:
Dividimos, entonces, entre el coeficiente de $ \frac{dy}{dx}$, que es “$ x+1$”, los coeficientes de los demás términos de la ecuación que dependen de “x”. Simplificamos.
$ \frac{dy}{dx}+P\left( x \right)y=f(x)$
$ \frac{dy}{dx}+\frac{x+2}{x+1}y=\frac{2x{{e}^{-x}}}{x+1}$
II. En el segundo paso encontramos el factor integrante:
$ {{\mathbf{e}}^{{\int }^{}\mathbf{P}\left( \mathbf{x} \right)\mathbf{dx}}}$,
Para esto sustituimos el valor de $P(x)$ en $ {{e}^{{\int }^{}P\left( x \right)dx}}$, donde:$ P(x)=\frac{x+2}{x+1}$. Para recordar las formulas integrales y el manejo de las funciones trascendentes y la división entre polinomios, vea el final del ejercicio.
$ {{e}^{{\int }^{}\frac{x+2}{x+1}dx}}={{e}^{{\int }^{}\text{dx}+{\int }^{}\frac{1}{x+1}dx}}$
$ ={{e}^{x+\ln (x+1)}}$
$ ={{e}^{x}}{{e}^{\ln (x+1)}}$
$ =\left( \text{x}+1 \right){{e}^{x}}$
III. Como tercer paso, encontramos la familia de soluciones del sistema homogéneo asociado:
Recordemos que el sistema homogéneo asociado, en este caso, es la ecuación diferencial:$ \frac{dy}{dx}+\frac{x+2}{x+1}y=0$ . Para resolverla sustituimos en la fórmula: $ {{y}_{c}}=C{{e}^{-{\int }^{}P\left( x \right)dx}}$, los valores de $ P(x)=\frac{x+2}{x+1}$, encontrado en el primer paso, y desarrollamos. Para esclarecer de donde sale la fórmula $ {{y}_{c}}=C{{e}^{-{\int }^{}P\left( x \right)dx}}$, siga el siguiente enlace: Solución del sistema homogéneo asociado.
$ {{y}_{c}}=C{{e}^{-{\int }^{}\frac{x+2}{x+1}dx}}$
$ =C{{e}^{{\int }^{}\text{dx}-{\int }^{}\frac{1}{x+1}dx}}$
$ =C{{e}^{-\text{x}-\ln (x+1)}}$
$ =C{{e}^{-\text{x}+\ln {{(x+1)}^{-1}}}}$
$ =C{{e}^{-\text{x}}}{{e}^{\ln {{(x+1)}^{-1}}}}$
$ =C{{(x+1)}^{-1}}{{e}^{-\text{x}}}$
$ =C\frac{{{e}^{-\text{x}}}}{(x+1)}$
Grafica de la familia de soluciones del sistema homogeneo asociado:
$ {{y}_{c}}=\frac{C{{e}^{-\text{x}}}}{(x+1)}$
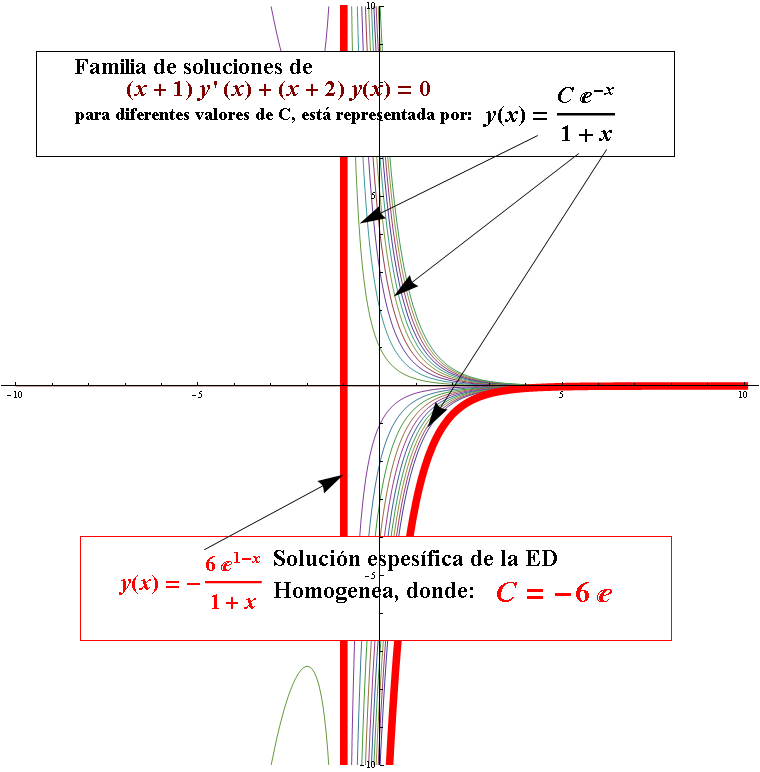
Se puede ver una solución particular $ y=-\frac{6{{e}^{1-x}}}{1+x}$ donde $ C=-6e$. Notar que la función
$ {{y}_{c}}=\frac{C{{e}^{-\text{x}}}}{(x+1)}$ , tiene como dominio el intervalo: $ -1\le x\le \infty $ (analizar el denominador de la función $ \frac{C{{e}^{-\text{x}}}}{(x+1)}$, pues aunque se nota una gráfica que aparece antes de -1 (gráfica en verde), esta también está indefinida en -1, por eso el intervalo más largo de definición de UNA solución es: $ (-1~,\infty )$. El intervalo de definición de una solución, por definición (ver Intervalo de definición de una solución I), necesita cumplir al menos 2 criterios para ser considerado válido: 1. Que la función solución que se encuentra esté definida en él (no necesariamente continua, una función definida por partes también puede calificar), y 2. Que esta función sea, también, derivable dentro del intervalo.
IV. En el cuarto paso, encontramos una solución particular a partir del sistema no homogéneo:
El sistema no homogéneo, en este caso, es la ecuación diferencial: $ \frac{dy}{dx}+\frac{x+2}{x+1}y=\frac{2x{{e}^{-x}}}{x+1}$, que representa la familia de soluciones particulares de la ED lineal. Para resolverla utilizamos la fórmula: $ {{y}_{p}}=\frac{1}{{{e}^{{\int }^{}P\left( x \right)dx}}}{\int }^{}{{e}^{{\int }^{}P\left( x \right)dx}}f(x)dx$, donde: $ {{e}^{{\int }^{}P\left( x \right)dx}}=\left( \text{x}+1 \right){{e}^{x}}$ (obtenido en el punto ii.) y $ f\left( x \right)=\frac{2x{{e}^{-x}}}{x+1}$ obtenido en el punto iPara ver de dónde salen estas siga el enlace siguiente: solución del sistema no homogeneo.
$ {{y}_{p}}=\frac{1}{\left( \text{x}+1 \right){{e}^{x}}}{\int }^{}\left( \text{x}+1 \right){{e}^{x}}\frac{2x{{e}^{-x}}}{x+1}dx$
$ =\frac{1}{\left( \text{x}+1 \right){{e}^{x}}}{\int }^{}2xdx$
$ =\frac{2}{\left( \text{x}+1 \right){{e}^{x}}}{\int }^{}xdx$
$ =\frac{2}{2\left( \text{x}+1 \right){{e}^{x}}}{{x}^{2}}$
$ =\frac{{{x}^{2}}{{e}^{-x}}}{\left( \text{x}+1 \right)}$
$ y=C\frac{{{e}^{-x}}}{(x+1)}+\frac{{{x}^{2}}{{e}^{-x}}}{\left( x+1 \right)}$
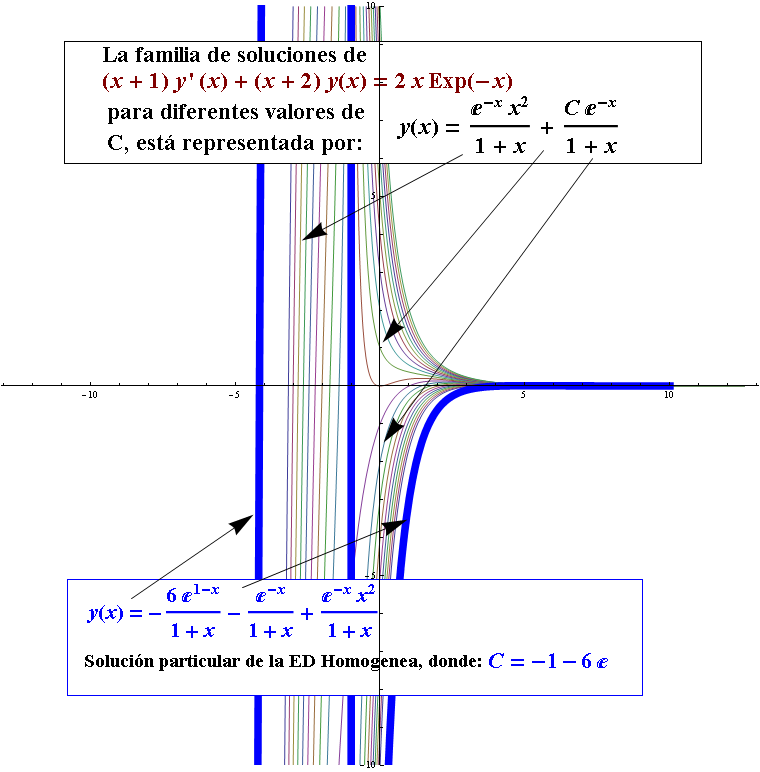
Se puede ver una solución particular $y\left( x \right)=-\frac{6{{\text{e}}^{1-x}}}{1+x}-\frac{{{\text{e}}^{-x}}}{1+x}+\frac{{{\text{e}}^{-x}}{{x}^{2}}}{1+x}$, Donde: $ C=-1-6e$. Nuevamente notar que la función $ y=C\frac{{{e}^{-x}}}{(x+1)}+\frac{{{x}^{2}}{{e}^{-x}}}{\left( x+1 \right)}$ , tiene como dominio el intervalo: $ (-1~,\infty )$. Por definición (ver Intervalo de definición de una solución I), el intervalo que contiene la solución de una ED, debe cumplir con 2 criterios: que la función esté definida y sea derivable en dicho intervalo.
Por tanto, la solución general de la ecuación diferencial $ (\text{x}+1)\frac{dy}{dx}+\left( x+2 \right)y=2x{{e}^{-x}}$, es:
$ y=C\frac{{{e}^{-x}}}{(x+1)}+\frac{{{x}^{2}}{{e}^{-x}}}{\left( x+1 \right)}$
Ecuación Diferencial Ejercicios Resueltos Dennis G. Zill cap 2.3. Prob 19
Recordar:
Logaritmos y exponenciales
$a\ln x=\ln {{x}^{a}}$
Debido a que:
$ y={{e}^{x}}$implica $ x=\ln y$ y además $ \ln y={{\log }_{e}}y$ recordamos que la función $ x={{\log }_{e}}y$, es inversa de $ y={{e}^{x}}$, por tanto si multiplicamos esta última función por ln obtendremos:
$ \ln y=\ln {{e}^{x}}=x$ y
$ {{e}^{x}}={{e}^{\ln y}}=y$
División entre Polinomios
$ \frac{x+2}{x+1}=1+\frac{1}{x+1}$
Ya que:
$ x+1\overset{1}{\overline{\left){\frac{x+2}{\frac{-x-1}{1}}}\right.}}$
Lo que intenté escribirles es el algoritmo de la división, el “1”en la parte superior (sobre la “x”), es el entero resultante de dividir $ \frac{x}{x}=1$, este es el “1” que usamos como parte del resultado, la línea debajo de $ x+2$, es el resultado de multiplicar el “1” de la parte superior por $ x+1$ e ir acomodando los términos debajo de sus correspondiente del dividendo, que en este caso es el mencionado término: $ x+2$, al final, al cambiarle los signos a este resultado y sumarlos al mismo dividendo vemos que: $ x+2-x-1=1$, este “1” es el que aparece hasta abajo, es el residuo, el cual es, junto con el divisor, la fracción: $ \frac{1}{x+1}$, sumada al final.
Para que obtengas la confianza necesaria en tu vida PROFESIONAL y en tu persona realiza ejercicios de aplicación y practica
- Realiza Modelado Matemático
- Aplica los algoritmos de solución. Te enseñamos a saber:
- ¿Por donde Empezar cuando tengo una ED enfrente?
- ¿Qué tipo de Ecuacion Diferencial tengo enfrente?
- ¿Qué método emplear para resolve la ED que tengo enfrente?
- Realiza simulación por computadora (simbólica y numérica) para transformar tu realidad y la de tu entorno, brindando servicio efectivo y sintiendote realizado como ingeniero, como matemñatico aplicado
- Inscríbete a nuestro PROGRAMA COMPLETO de ECUACIONES DIFERENCIALES

Aplicaciones de las Ecuaciones Diferenciales

Yo puedo participar dese material.
Vc
Hola Victor, espero que estés muy bien, Feliuz Año Nuevo.
Puedes utilizar todo el material que halles en este blog, Victor.
Si te refieres al material del Progrma completo, que es un progama de transformación, puedes hacerlo, el costo a partir del 3 de enero será de 145 usd, es un programa que te llevara al siguiente nivel de expertise, y te tengo una buena noticia, si pagas hoy o mañana antes de la noche, te tengo un supr descuento del 69%, si te interesa mandame un mensaje directo al buzón de nuestra página de fans y te doy toda la información, acá el enlace: Ecuaciones Diferenciales Ejercicios y Aplicaciones
Saludos y espero tu mensaje, nos vemos Victor.