Ecuacion Diferencial lineal homogénea y su sistema no homogéneo; de 1er orden

Con el método de los 4 pasos que puedes encontrar en este link: ED lineal de 1er orden, click aquí, podrás resolver cualquier ecuacion diferencial lineal homogenea.

Te recomiendo que uses el método varias veces antes de entrar a la teoría, pues la mente necesita estar acostumbrada a manejar la simbología, el álgebra y la secuencia de cualquier método para posteriormente poder entenderlo con éxito. Esto lo saque de las corrientes de aprendizaje holístico, PNL y neurociencias como el curso: Learn More, Study Less: The Video Course, del Autor Scott Young.

Método: Factor Integrante (ver enlace)

Ejercicios 2.3 Libro Dennis G. Zill (Problema 24). Tomado de: Dennis G. Zill Ed 7ma.

Sustituimos el valor de P($x$) en ${{e}^{\mathop{\int }^{}P\left( x \right)dx}}$, $P(x)=\frac{2}{{{x}^{2}}-1}$. El desarrollo de la las fracciones parciales se muestra al final del ejercicios, así como las formulas integrales y el manejo de las funciones trascendentes.

${{e}^{2\mathop{\int }^{}\frac{dx}{{{x}^{2}}-1}}}={{e}^{2\mathop{\int }^{}[\frac{1}{2\left( x-1 \right)}-\frac{1}{2\left( x+1 \right)}]dx}}$

$={{e}^{2\mathop{\int }^{}\frac{dx}{2\left( x-1 \right)}-2\mathop{\int }^{}\frac{dx}{2\left( x+1 \right)}}}$

$={{e}^{\mathop{\int }^{}\frac{dx}{\left( x-1 \right)}-\mathop{\int }^{}\frac{dx}{\left( x+1 \right)}}}$

$={{e}^{\ln |x-1|-\ln |x+1|}}$

$={{e}^{\ln \frac{|x-1|}{|x+1|}}}$

$=\frac{x-1}{x+1}$

III.                    Como tercer paso, encontramos la familia de soluciones del sistema homogéneo asociado:

El sistema homogéneo asociado es la ecuación diferencial:$\frac{dy}{dx}+\frac{2}{{{x}^{2}}-1}y=0$. Sustituimos en la fórmula: ${{y}_{c}}=C{{e}^{-\mathop{\int }^{}P\left( x \right)dx}}$, los valores de $P(x)=\frac{2}{{{x}^{2}}-1}$, encontrado en el primer paso,  y desarrollamos. Notar que el resultado de ${{y}_{c}}$, es el recíproco del factor integrante multiplicado por C. Para esclarecer de donde sale la fórmula ${{y}_{c}}=C{{e}^{-\mathop{\int }^{}P\left( x \right)dx}}$, siga el siguiente enlace: Solución del sistema homogéneo asociado.

Gráfica de la familia de soluciones del sistema homogeneo asociado:

${{y}_{c}}=C\frac{x+1}{x-1}$

Se puede ver una solución particular ${{y}_{c1}}=\frac{2(x+1)}{x-1}$ donde $C=2$. Notar que la función ${{y}_{c}}=C\frac{x+1}{x-1}$  , tiene como dominio más largo el intervalo: $1<x<\infty $. Sin embargo, debido a la no definición de la gráfica en $-1 < x < 1$, se puede tomar éste intervalo para hacer evidente ésta no definición. El intervalo más largo de definición de UNA solución es: $(1, \infty )$. El intervalo de definición de una solución, por definición (ver: Intervalo de definición de una solución I), necesita cumplir al menos 2 criterios para ser considerado válido: 1. Que la función solución que se encuentra esté definida en él (no necesariamente continua, una función definida por partes también puede calificar), y 2. Que esta función sea, también, derivable dentro del intervalo.

El sistema no homogéneo es: $\frac{dy}{dx}+\frac{2}{{{x}^{2}}-1}y=\frac{x+1}{x-1}$, que representa la familia de soluciones particulares de la ED lineal. Para resolverla utilizamos la fórmula: ${{y}_{p}}=\frac{1}{{{e}^{\mathop{\int }^{}P\left( x \right)dx}}}\mathop{\int }^{}{{e}^{\mathop{\int }^{}P\left( x \right)dx}}f(x)dx$, donde: ${{e}^{\mathop{\int }^{}P\left( x \right)dx}}=\frac{x-1}{x+1}$ (obtenido en el punto ii.) y $f\left( x \right)=\frac{x+1}{x-1}$ obtenido en el punto i. Para ver de dónde salen estas siga el enlace siguiente: solución del sistema no homogéneo.

${{y}_{p}}=\frac{x+1}{\text{x}-1}\mathop{\int }^{}\frac{x-1}{x+1}(\frac{x+1}{x-1})dx$

$=\frac{x+1}{\text{x}-1}\mathop{\int }^{}dx$

$=\frac{x+1}{\text{x}-1}[x]$

$=\frac{x(x+1)}{\text{x}-1}$

Gráfica de la familia de soluciones del sistema no homogéneo:

$y=\frac{C(x+1)}{x-1}+\frac{x(x+1)}{x-1}$

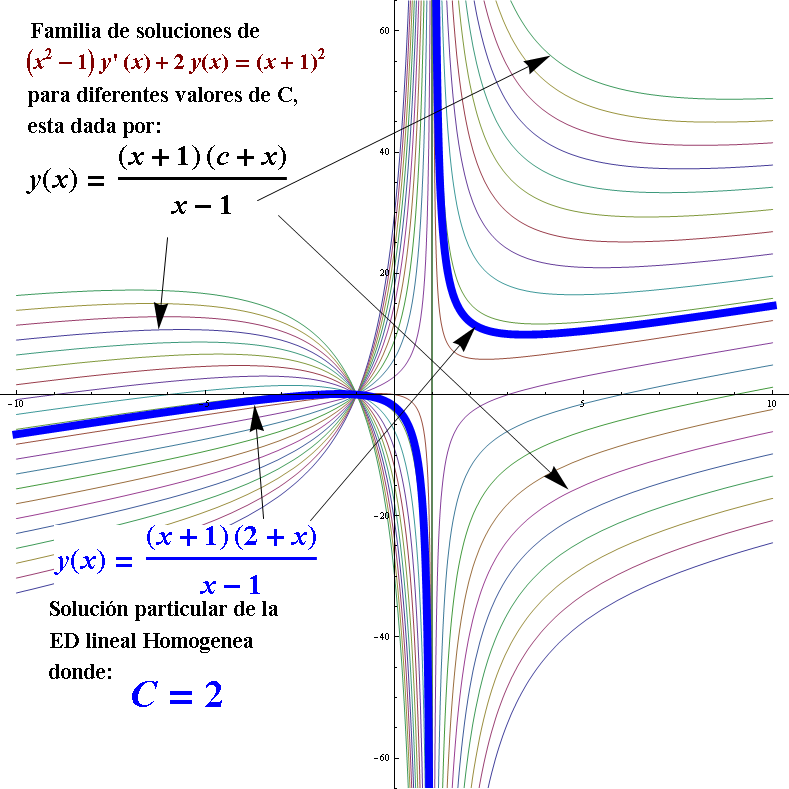
Se puede ver una solución particular $\text{y}\left( \text{x} \right)=\frac{(x+1)(2+x)}{x-1}$,

Donde: $C=2$. Nuevamente notar que la función $y=\frac{C(x+1)}{x-1}+\frac{x(x+1)}{x-1}$ , tiene como dominio el intervalo: $(-1,1)$ y como dominio. Por definición (ver Intervalo de definición de una solución I), el intervalo que contiene la solución de una ED, debe cumplir con 2 criterios: que la función esté definida y sea derivable en dicho intervalo.

Por tanto, la solución general de la ecuación diferencial $({{x}^{2}}-1)\frac{dy}{dx}+2y={{(x+1)}^{2}}$, es:

$y=\frac{(c+x)(x+1)}{x-1}$

Con intervalo de solución:

Nota: $c$ puede ser negativa si se toma el valor negativo del valor absoluto del logaritmo en el paso III.

$\Large I:\left \{ x\epsilon \mathbb{R}\mid -1< x< 1 \right \}$

Recordar:

Fraciones parciales

$\frac{1}{{{x}^{2}}-1}=\frac{A}{x-1}+\frac{B}{x+1}$

$=A\left( x+1 \right)+B(x-1)$

$=Ax+A+Bx-B$

$=(A+B)x+A-B$

Igualando los términos semejantes de la derecha con los de la izquierda.

No hay términos en “x” así que:

$A+B=0$ $\Rightarrow A=-B$

Para las variables A, B solas, está el “1”

$A-B=1$  $\Rightarrow A=1+B$

Por tanto:

$-B=1+B$

$2B=-1$

$B=-\frac{1}{2}$ $\Rightarrow A=\frac{1}{2}$

De donde:

$\frac{1}{{{x}^{2}}-1}=\frac{\frac{1}{2}}{x-1}-\frac{\frac{1}{2}}{x+1}$

$\frac{1}{{{x}^{2}}-1}=\frac{1}{2(x-1)}-\frac{1}{2(x+1)}$

Logaritmos y exponenciales

$a\ln x=\ln {{x}^{a}}$

Debido a que:

$y={{e}^{x}}$ implica  $x=\ln y$ y además $\ln y={{\log }_{e}}y$ recordamos que la función $x={{\log }_{e}}y$, es inversa de $y={{e}^{x}}$, por tanto si multiplicamos esta última función por ln obtendremos:

$\ln y=\ln {{e}^{x}}=x$   y

${{e}^{x}}={{e}^{\ln y}}=y$