Encontrar el intervalo de solución para un Problema del Valor Inicial la solución, siendo dicho intervalo de solución «I», el intervalo más largo , para el Problema del Valor Inicial:
a) $\frac{dT}{dt}=k(T-Tm)$, $T(0)={{T}_{0}}$
Utilizaremos el método del Factor Integrante (ver enlace), mediante los 4 pasos que hemos utilizamos aquí para resolver cualquier ED lineal de 1er orden (link: Método de los 4 pasos)
Ejercicios 2.3 Libro Dennis G. Zill, Ed 7ma. (Problema 28).
Pasos:
I. El primer paso consiste en escribir la forma estándar de la ED a resolver:
Multiplicamos el lado derecho de la ecuación y agrupamos, para obtener la forma estándar. Note que , es una constante.
$\frac{dT}{dt}+P\left( t \right)T=f(t)$
$\frac{dT}{dt}-kT=-k{{T}_{m}}$
II. En el segundo paso encontramos el factor integrante: ${{\mathbf{e}}^{\mathop{\int }^{}\mathbf{P}\left( t \right)\mathbf{dt}}}$,
El valor de $P(x)$ en ${{e}^{\mathop{\int }^{}P\left( t \right)dt}}$ , es: $P\left( t \right)=-k$.
${{e}^{-k\mathop{\int }^{}dt}}={{e}^{-kt}}$
III. Como tercer paso, encontramos la familia de soluciones del sistema homogéneo asociado:
El sistema homogéneo asociado es :$\frac{dT}{dt}-kT=0$. Sustituimos en ${{T}_{c}}=C{{e}^{\mathop{\int }^{}P(t)dt}}$, donde: $P\left( t \right)=-k$ encontrado en el primer paso, y desarrollamos. Para esclarecer de donde sale la fórmula ${{T}_{c}}=C{{e}^{-\mathop{\int }^{}P\left( t \right)dt}}$, siga el siguiente enlace: Solución del sistema homogéneo asociado.
${{T}_{c}}=C{{e}^{(-)-k\mathop{\int }^{}dt}}$
$=C{{e}^{kt}}$
Solución Específica para el Sistema Homogéneo
Para encontrar una solución específica para el sistema homogéneo, utilizaremos los valores iniciales de $\text{t}=0;\text{ }\!\!~\!\!\text{ }\!\!~\!\!\text{ }\!\!~\!\!\text{ }T={{T}_{0}}$ , de modo que:
Sustituyendo en:
${{T}_{c}}=C{{e}^{kt}}$
Tenemos:
${{T}_{0}}=C{{e}^{k(0)}}~\Rightarrow ~~{{T}_{0}}=C\left( 1 \right)~~\Rightarrow ~~C={{T}_{0}}$
Por tanto, la solución particular (específica) del sistema homogéneo asociado es:
${{T}_{c1}}={{T}_{0}}{{e}^{kt}}$
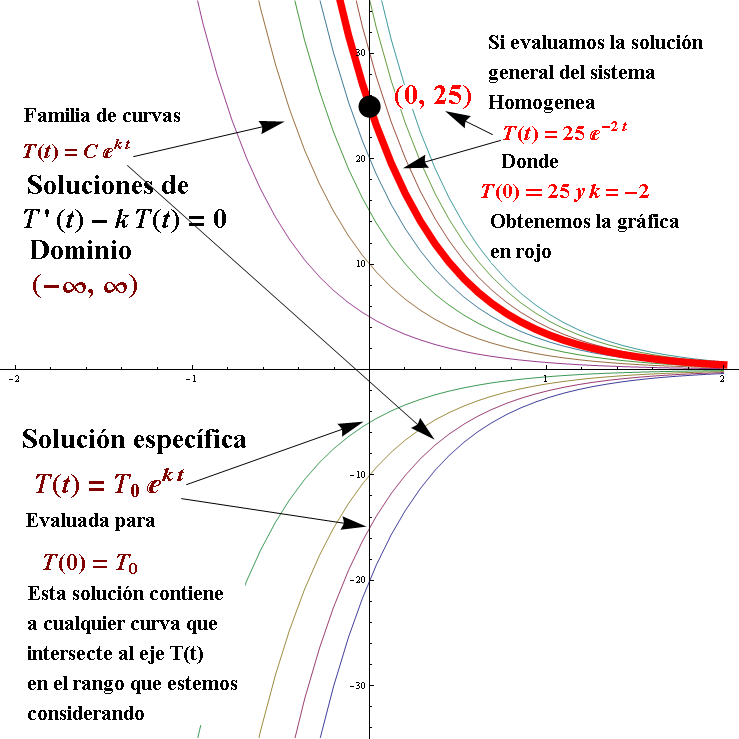
Grafica de la familia de soluciones del sistema homogeneo asociado:
${{T}_{c}}=C{{e}^{kt}}$ y la solución particular ${{T}_{c1}}={{T}_{0}}{{e}^{kt}}$
La función ${{T}_{c}}=C{{e}^{kt}}$ , tiene como dominio el intervalo:
$D_{T_{C}}:\left \{ t\epsilon R\mid -\infty < t< \infty \right \}$
Por tanto, la solución particular $T_{c1}=T_{0}e^{kt}$, tiene el mismo dominio:
$D_{T_{C1}}:\left \{ t\epsilon R\mid -\infty < t< \infty \right \}$
Notar que la solución particular solo involucra a las curvas que intersectan a $T(t)$, dentro del rango que estemos analizando. El valor de $C={{T}_{0}}$ , para la solución particular del PVI $\frac{dT}{dt}=kT$, $T(0)={{T}_{0}}$. El intervalo de definición de una solución, por definición (ver Intervalo de definición de una solución I), necesita cumplir al menos 2 criterios para ser considerado válido: 1. Que la función solución que se encuentra esté definida en él (no necesariamente continua, una función definida por partes también puede calificar), y 2. Que esta función sea, también, derivable dentro del intervalo.
IV. En el cuarto paso, encontramos una solución particular a partir del sistema no homogéneo:
El sistema no homogéneo es: $\frac{dT}{dt}-kT=-k{{T}_{m}}$. Para resolverla utilizamos la fórmula: ${{T}_{p}}=\frac{1}{{{e}^{\mathop{\int }^{}P\left( t \right)dt}}}\mathop{\int }^{}{{e}^{\mathop{\int }^{}P\left( t \right)dt}}f(t)dt$, donde: ${{e}^{\mathop{\int }^{}P\left( t \right)dt}}={{e}^{-kt}}$ (obtenido en el punto ii.) y $f\left( t \right)=-k{{T}_{m}}$ obtenido en el punto i. Para ver de dónde salen estas siga el enlace siguiente: solución del sistema no homogeneo.
${{T}_{p}}=\frac{1}{{{e}^{-kt}}}\mathop{\int }^{}{{e}^{-kt}}(-k{{T}_{m}})dt$
$=\frac{{{T}_{m}}}{{{e}^{-kt}}}\mathop{\int }^{}{{e}^{-kt}}(-k)dt$
$=\frac{{{T}_{m}}}{{{e}^{-kt}}}[{{e}^{-kt}}]$
$={{T}_{m}}$
Solución del Problema de Valores Iniciales (PVI) de la ED lineal de 1er Orden
La solución del problema del PVI se obtiene al encontrar una solución específica que cumpla con las condiciones iniciales (que las contenga), del problema. Para esto, necesitamos encontrar el valor de “C”, de la solución general, sustituyendo en la solución general, los valores de “t” e “i”, que vienen como condiciones iniciales y despejando “C”.
$t=0;~~~~~~T={{T}_{0}}$
Por tanto:
Si la solución general del Sistema no Homogéneo es:
$T\left( t \right)=C{{e}^{kt}}+{{T}_{m}}$
Entonces, sustituyendo los valores iniciales
$T\left( 0 \right)={{T}_{0}}$
Tenemos:
${{T}_{0}}=C{{e}^{k(0)}}+{{T}_{m}}$
$\Rightarrow {{T}_{0}}=C(1)+{{T}_{m}}$
$\Rightarrow C={{T}_{0}}-{{T}_{m}}$
Por lo que UNA solución particular del sistema no Homogéneo, es:
$T\left( t \right)=({{T}_{0}}-{{T}_{m}}){{e}^{kt}}+{{T}_{m}}$
Gráfica de la familia de soluciones del sistema no homogéneo:
$T\left( t \right)=C{{e}^{kt}}+{{T}_{m}}$
y la solución particular del PVI:
$T\left( t \right)=({{T}_{0}}-{{T}_{m}}){{e}^{kt}}+{{T}_{m}}$
El dominio de la solución $T\left( t \right)=({{T}_{0}}-{{T}_{m}}){{e}^{kt}}+{{T}_{m}}$ está en el intervalo:
${{D}_{i(t)}}:-\infty <t< \infty$
O dicho de forma más común, el dominio de la solución del PVI ($\frac{dT}{dt}=k(T-Tm)$, $T(0)={{T}_{o}}$ ), es el intervalo: $(-\infty ,\infty )$. Notar que el valor de $C={{T}_{0}}-Tm$ , para el problema del PVI.
Por tanto, la solución del Problema del Valor Inicial:
$\frac{dT}{dt}=k(T-Tm)$, $T(0)={{T}_{0}}$, es,
$T\left( t \right)=({{T}_{0}}-{{T}_{m}}){{e}^{kt}}+{{T}_{m}}$
Con intervalo de solución:
$D_{T_{C}}:\left \{ t\epsilon R\mid -\infty < t< \infty \right \}$
Intervalo de solución para un Problema del Valor Inicial: Analizando dos casos espacíficos
Para analizar el comportamiento de dos casos particulares de variación de T(t), con respecto del tiempo, mostramos las siguientes tablas y gráficas.
Sistema representado por: $T\left( t \right)=25{{\text{e}}^{-2t}}$
En esta gráfica podemos ver que mientras $t\to \infty $, $T\left( t \right)\to 0$. Se trata de un proceso de descongelamiento y la temperatura se tiende a estabilizar, en este caso a CERO, por tratarse de un sistema Homogéneo; hablando de sistemas físicos representados mediante Ecuaciones Diferenciales, cuando la función $f\left( x \right)=0$, se refiere, en general a que no existen factores externos al sistema que lo modifiquen. Veamos el siguiente ejemplo:
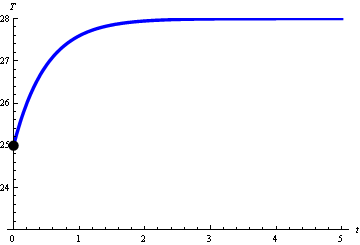
Sistema representado por: $T\left( t \right)={{\text{e}}^{-2t}}(-3+28{{\text{e}}^{2t}})$
En este ejemplo el sistema recibe los efectos del medio ambiente al involucrarse la variable $Tm=28$. Notar que $f\left( x \right)=-kTm$, en la ecuación original: $\frac{dT}{dt}=k(T-Tm)$. En este caso, el sistema incrementa su temperatura cuando “t” aumenta. La temperatura de estabilidad es $Tm=28$. Esto se puede ver más claro en la gráfica de “Campo de direcciones”
En el análisis de fenómenos físicos modelados con Ecuaciones Diferenciales en la actualidad es importante contar con un software que te permita obtener resultados tanto de las técnicas de Graficación, como de las técnicas de simulación numérica, es por eso que en este Blog he integrado la página: Haz Tu Simulación (da click aquí), donde podrás escribir tu código en los programas: Octave, Máxima, Python o SAGE, para simular y/o graficar tus modelos de ecuaciones diferenciales.
Intervalo de solución para un Problema del Valor Inicial: Cómo realiza simulaciones con software matemático de código abierto
Las simulaciones por computadora de los sismetas dinámicos modelados matemáticamente (con ecuaciones diferenciales), son imprescindibles, no solo para comprender mejor los conceptos aprendidos, si no para poder pronosticar comportamientos y tomar decisiones; todo ingeniero o científico necesita de los conociemientos para realizarlas.
En mi curso Ecuaciones Diferenciales con SAGE, te llevo paso a paso para que aprendas a simular cada tipo de ecuación diferencial así como poder reunir ese conocimiento mediante un proyecto final en donde desarrolamos la simulación de un sistema físico real. 😉
Para tener un conocimieto básico de cómo realizar las simulaciones de ecuaciones lineales en SAGE, visita la siguiente página: Cómo simular con SAGE.
Intervalo de solución para un Problema del Valor Inicial: Cómo aprender ED’s
La intuición y la confianza son parte importantes en el aprendizaje de esta materia, es por eso que para desarrollarlas será necesario practicar varias veces con los métodos y técnicas aquí descritos teniendo una actitud mental apropiada. Para que conozcas la actitud mental que me ha hecho prosperar en esta y otras materias a lo largo de mi vida, te comparto el artículo: La técnica perfecta para aprender Ecuaciones Diferenciales, donde te revelo la actitud que me ha hecho tener éxito en materias arduas pero fascinantes como esta.
Por último te recomiendo revises los productos que me han servido en mis propios estudios; están al final del artículo: La técnica perfecta para aprender Ecuaciones Diferenciales, bajo el apartado Técnicas perfectas para aprender. Estoy seguro te servirán. 🙂
Encontraste la información que buscabas?
Necesito otros ejemplos: ejercicio 27, ejercicio 29
Para cualquier duda sobre los ejercicios resueltos o el sitio WEB te invito a dejar un comentario o contáctame en esta página: Contacto(da click aquí)