Circuito electrico mixto y ecuaciones diferenciales. Circuitos Eléctricos RLC en serie
En el siguiente artículo aprenderás mediante un ejemplo cómo se resuelve un circuito electrico mixto o circuito electrico RLC utilizando ecuaciones diferenciales y conocerás la relación entre los componentes del circuito y su representación como cantidades diferenciales que cambian con el tiempo.
Para desarrollar este ejemplo partiremos de la configuración básica para un circuito RLC, que es cuando sus componentes están conectados en serie, como lo muestra la Figura 1.
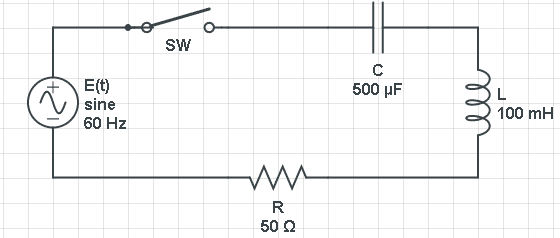
Donde, los elementos mostrados son:
- Un resistor con una resistencia $ R$ ohms
- Un inductor con una inductancia de $ L$ henries,
- Un capacitor con una capacitancia de $ C$ faradios,
- Una fuente de Corriente Alterna que suministra un voltaje $ E(t) $de $ 110$ V
- a $ 60$ Hz, en el tiempo $ t$.
De acuerdo con los principios elementales de electricidad, las caídas de voltaje a través de los elementos del circuito son las que se muestran en la Tabla 1.
| Elementos del circuito | Símbolo | Caída de Voltaje(representación diferencial) | Valores |
| Inductor | $ L$ | $ L\frac{dI}{dt}$ | $ 100$ mH |
| Resistor | $ R$ | $ RI$ | $ 50$ Ω |
| Capacitor | $ C$ | $ \frac{1}{C}Q$ | $ 500$ μF |
| Fuente de corriente alterna | $ E(t)$ | Voltaje suministrado en el tiempo $ t$ | $ 110$ V a 60Hz |
Estas expresiones, para las caídas de voltaje, derivadas de la física, provienen de conclusiones experimentales, que han llevado a las siguientes definiciones:
Caídas de Voltaje. Circuito electrico mixto
- Resistencia. La caída de voltaje a través de una resistencia ($ R$) es proporcional a la corriente que pasa a través de ésta, es decir: $ E(t) \alpha I$ ó $ E(t) =R I$ (Ley de Ohm). Donde $ R$ es la constante de proporcionalidad llamada coeficiente de resistencia o simplemente resistencia.
- Inductor. La caída de voltaje a través de un inductor es proporcional a la tasa de tiempo instantánea de cambio de la corriente, es decir: $ E(t) \alpha\frac{d{I}}{d{t}}$ ó $ E(t) = L \frac{d{I}}{d{t}}$. Donde $ L$ es la constante de proporcionalidad llamada el coeficiente de inductáncia o simplemente inductor.
- Capacitor (condensador). La caída de voltaje a través de un condensador es proporcional a la carga eléctrica instantánea en el condensador: $ E(t) \alpha Q$ ó $ E(t) =\frac{{Q}}{C}$. Donde $ \frac{1}{C}$ es la constante de proporcionalidad y $ C$ es la capacitancia del capacitor o inductor.
Estas definiciones se pueden entender mejor si guardamos en mente que una resistencia disipa una parte de corriente como calor, un inductor se opone a los cambios de corriente por el efecto del campo magnético que genera alrededor de sí que a su vez le autoinduce una tensión, un capacitor (condensador), es un elemento que almacena energía.
La Ecuación Diferencial que representa un circuito RLC conectado en serie.
Todos los elementos del Circuito RLC de este ejemplo están conectados en serie con la fuerza Electromotriz que suministra el voltaje de $ E(t)$ en el tiempo $x t$, como lo muestra la Figura 1. Si el interruptor mostrado en la Figura 1, se cierra, esto provoca una corriente $ I(t)$ en amperes en el circuito y una carga $ Q(t)$ en coulombs en el capacitor en el tiempo $ t$. La relación entre las funciones $ I$ y $ Q$ es:
| \begin{equation} \frac{dQ}{dt} = I(t) \end{equation} | (1) |
Es decir:
La corriente eléctrica o intensidad eléctrica es el flujo de carga (eléctrica) por unidad de tiempo que recorre un material.
Esta relación se deriva de la relación entre la corriente y la carga crecientes, que se obtienen de la experimentación. Las unidades utilizadas para esta ecuación pertenecen al sistema $ mks$, por lo que la unidad de tiempo es el segundo(s).
Para modelar matemáticamente el circuito de la Figura 1, utilizamos una de las leyes de Kirchoff -la aplicada a mallas-, las cuales se basan en la conservación de la energía y la carga aplicada a circuitos eléctricos.
Ley de Kirchoff (mallas)
La suma (algebraica) de las caídas de voltaje a través de los elementos en una malla cerrada de un circuito eléctrico es igual al voltaje aplicado.
Ecuación Diferencial para un circuito eléctrico mixto RLC
De modo que, sumando las caídas de voltaje (ver Tabla 1) e igualándolas al voltaje de la fuente de corriente alterna, tenemos:
| \begin{equation} L \frac{d\mathbf{I}}{d{t}} +{R}{I}+ \frac{1}{C} \mathbf{Q}= E ( t) \end{equation} | (2) |
Podemos notar que si sustituimos las ecuaciones (1) y (2), para tener solo una función como incógnita (digamos $ Q$), obtenemos:
| \begin{equation} L \frac{d^2 {Q}}{d{t}^2} +{R} \frac{d{Q}}{d{t}} + \frac{1}{C} {Q}= E ( t) \end{equation} | (3) |
Con lo que tenemos una expresión consistente para el circuito RLC conectado en serie como el mostrado en la Figura 1.
Ahora, si derivamos la ecuación (3) en ambos lados, sustituyendo $ {I}$ por $ {Q}’$ obtenemos:
| \begin{eqnarray*} L \frac{d^2{I}}{d{t}^2} +{R}\frac{d{I}}{d{t}} + \frac{1}{C} \ast\frac{d}{d{t}} \int {I}d{t} & = & E’ ( t) \end{eqnarray*} |
ya que:
| \begin{eqnarray*} \frac{d{Q}}{d{t}} & = & {I} ( t)\\\\ \int d{Q} & = & \int {I} ( t) d{t}\\\\ {Q} & = & \int {I} ( t) d{t} \end{eqnarray*} |
Es decir:
| \begin{equation} L \frac{d^2 {I}}{d{t}^2} +{R} \frac{d{I}}{d{t}} + \frac{1}{C} {I}= E’ ( t) \end{equation} | (4) |
De esta forma tenemos las ecuaciones (3) y (4), para resolver nuestro problema ejemplo, que a continuación describo.
Circuito electrico mixto y ecuaciones diferenciales. Aplicaciones.
Ecuación Diferencial Aplicada a un Circuito Eléctrico tipo RLC de 2º Orden
Ejemplo:
Considere un circuito RLC con $ R = 50 {ohms} ({\Omega})$, $ L =0.1 {henry} ( H)$ y $ C = 5 \times 10^{- 4} {farad} ( F)$. En el tiempo $ t=0$, cuando tanto $ {I}(0)$ como $ {Q}(0)$ son cero, el circuito se conecta a un generador de corriente alterna de $ 110 {Volts}, 60 {Hz}$. Encuéntrese la corriente en el circuito.
Solución:
Para resolver este problema recordemos lo siguiente:
El caso típico el voltaje de corriente alterna, se representa como:
| \begin{equation} E(t) = E_0 {sen} {\omega}{t} \end{equation} | (5) |
Donde, $ E_0$es el voltaje inicial (en el tiempo 0).
Solución de una ecuación diferencial lineal NO homogénea de 2º orden
La solución general de una ecuación diferencial lineal no homogénea de 2º orden, se compone de la suma de la solución de su sistema homogéneo asociado mas una solución particular, es decir la solución de una ecuación diferencial lineal no homogénea:
$ \Large {a}_2 y» +{a}_1 y’ +{a}_0 y = f ( x)$
Donde $ {a}_2$, ${a}_1$, ${a}_0$, son constantes.
Tiene la forma:
$ \large y = y_c + y_p$
Donde:
$ y$: solución general
$ y_c :$ es la solución complementaria o solución del sistema homogéneo asociado: $ {a}_2 y» +{a}_1 y’ +{a}_0 y = 0$
$ y_p$: es una solución particular o solución del sistema no homogéneo:
$ {a}_2 y» +{a}_1 y’ +{a}_0 y = f ( x)$
En circuitos eléctricos dicha solución tiene un significado físico por lo que para un circuito RLC respresentado por la ecuación diferencial de 2º orden (4): $ L \frac{d^2 {I}}{d{t}^2} +{R}\frac{d{I}}{d{t}} + \frac{1}{C} {I}= E’ ( t)$, la solución está compuesta por:
- Una Corriente Transitoria ($ {I}_{{tr}}$, derivada del sistema homogéneo asociado) más,
- Una Corriente Periódica Estacionaria ($ {I}_{{ps}}$, que es una solución particular derivada del sistema no homogéneo). De modo que, al solución de la Ecuación Diferencial (4), es:
| \begin{equation} {I}={I}_{{tr}} +{I}_{{ps}} \end{equation} | (6) |
Donde:
$ {I}$: Corriente total del circuito (solución general)
$ {I}_{{tr}}$: Corriente transitoria (equivalente a la solución $ y_c$ del sistema homogéneo)
$ {I}_{{ps}}$: Corriente periódica estacionaria (equivalente a la solución $y_p$ del sistema no homogéneo)
Solución de la Ecuación diferencial aplicada a un circuito electrico mixto RLC
Por tanto, analizando los datos tenemos:
Una frecuencia de 60Hz significa que $ {\omega}= ( 2{\pi}) (60) {rad} / {seg}$, ya que $ {\omega}= 2{\pi}f$. Lo cual equivale a $ {\omega}= 377 {rad}/{seg}$.
El voltaje de suministro es $ E_0 = 110$ Volts, de donde $ E ( t) = 110 {sen} 377{t}$.
De donde, utilizando la ecuación (4) y la derivada de la (5), obtenemos la ecuación diferencial que modela nuestro circuito RLC conectado en serie, con los datos proporcionados:
| \begin{eqnarray} L \frac{d^2 {I}}{d{t}^2} +{R} \frac{d{I}}{d{t}} + \frac{1}{C}{I} & = & {\omega}E_0 \cos {\omega}{t} \nonumber\\\\ ( 0.1) {I}» + 50{I}’ + 2000{I} & = & ( 377) ( 110) \cos 377{t} \end{eqnarray} | (7) |
Para resolver la ecuación (7), utilizamos los métodos de solución para ecuaciones diferenciales de orden superior, que a continuación describo:
Métodos de Solución de Ecuaciones Diferenciales de Orden Superior
Hemos de recordar que la solución de una Ecuación Diferencial es encontrar una función, a diferencia de lo que obteníamos al resolver una ecuación algebraica, donde el propósito era encontrar un valor (numérico) específico.
De este modo que al pensar en una solución habrá que pensar en encontrar la función que satisface la expresión matemática diferencial al obtener las derivadas que ésta indique.
Existen diferentes métodos para encontrar dicha función solución, para las ecuaciones diferenciales de Orden Superior, los métodos analíticos mas usados son:
– El método de la Ecuación Auxilar para Ecuaciones Lineales Homogeneas con Coeficientes Constantes. (Solo para resolver ED’s lineales homogéneas) El método para resolver este tipo de ecuaciones utiliza una ecuación auxiliar de la Ecuación Diferencial para «convetir» a ésta en una ecuación algebraica cuya solución es el valor para $ m_i$ de la función exponencial $ y_= e^{m_i x}$ y donde $ x$ es la variable independiente de la Ecuación Diferencial y $ y ( x)$, la variable dependiente.
– El método de Reducción de Orden para Ecuaciones Diferenciales homogéneas y NO homogéneas. Éste método se utiliza para encontrar una segunda solución cuando resulta una solución uniparamétrica, al resolver una ED lineal homegénea o No homogenea, por ejemplo, de 2o orden. Al estar resolviendo una ED lineal homogénea de 2o orden se utiliza la ecuación $ y(x)=y_{1}(x) \int \frac{e^{-\int P(x) dx}}{y^{2}(x)}$, para cuando se busca una segunda solución; para un ED lineal NO homogénea de 2o orden, se utiliza la ecuación: $ y(x)=u(x)y_{1}(x)$. Éste método, se puede utilizar para cuando los coeficientes de la Ecuación Diferencial, ya sea homogénea o no, son variables o constantes.
– El método de Superposición para Ecuaciones Diferenciales homogéneas y NO homogéneas. Éste es el método utilizado en éste artículo y muchas veces también utilizado en Electricidad y Electrónica para la solución de las Ecuaciones Diferenciales de 2o orden o superior. Ver el ejemplo.
– El método del Anulador para Ecuaciones Diferenciales homogéneas y NO homogéneas. Éste método es similar al anterior, solo que para determinar la solución particular se utiliza el operador $ D$ anulador
– El método de Variación de Parámetros. para Ecuaciones Diferenciales homogéneas y NO homogéneas. Éste método supone una solución no trivial que se multiplica por la solución conocida que resulta de resolver el sistema homogéneo asociado. Este método es básico para comprender algebraicamente el desarrollo de los métodos de solución arriba mencionados.
Entre otros métodos.
Dicho sea de paso el método de Variación de Parámetros proviene del TEOREMA de SUPERPOSICIÓN, el estudio del mismo aclara el método.
En el ejemplo que aquí desarrollamos, haremos uso de dos de los métodos mencionados. Partiendo de nuestro conocimiento de que la solución de la ecuación $ L \frac{d^2 {I}}{d{t}^2} +{R}\frac{d{I}}{d{t}} + \frac{1}{C}{I} ={\omega}E_0 \cos {\omega}{t}$, es la ecuación (6), vista con anterioridad:
$ \Large {I}={I}_{p{tr}} +{I}_{{ps}}$
Utilizaremos los siguientes Métodos de Solución para la Ecuación diferencial lineal de 2º orden (4), que representa a un circuito electrico mixto tipo RLC.
Encontraremos, $ {I}_{{tr}}$: mediante el método de la Ecuación Auxiliar para Ecuaciones Diferenciales Lineales Homogéneas con Coeficientes Constantes.
Encontraremos, $ {I}_{{ps}}$: mediante el método de Superposición para Ecuaciones Diferenciales NO homogéneas con Coeficientes Indeterminados.
Ecuaciones Diferenciales Lineales Homogéneas con Coeficientes Constantes
Con este conocimiento retomamos el ejemplo que estamos desarrollando para encontrar la Corriente Transitoria $ {I}_{{tr}}$, resolviendo la Ecuación Homogénea asociada de la Ecuación Diferencial (7), la cual es:
| \begin{equation} ( 0.1) {I}» + 50{I}’ + 2000{I}= 0 \end{equation} | (8) |
De donde, según el método de solución para Ecuaciones Lineales Homogéneas con Coeficientes Constantes, aplicado a un ecuación diferencial de 2º orden, necesitamos utilizar una ecuación auxiliar que nos permita encontrar el exponente $ m_i$ de las funciones $ y_1 = e^{m_1 x}$ y $ y_2 = e^{m_2 x}$, las cuales se toman como solución de la ecuación diferencial homogénea:
| \begin{equation} {a}_2 y» +{a}_1 y’ +{a}_0 y = 0 \end{equation} | (9) |
Donde $ {a}_2$, ${a}_1$, $ {a}_0$, son constantes.
(ver el link: método de solución para Ecuaciones Lineales Homogéneas con Coeficientes Constantes).
Para nuestro caso, las funciones solución buscadas son:
| $ I_{1} ( t) = e^{m_1 t}$ | (10) |
| $ I_{2} ( t) = e^{m_2 t}$ | (11) |
La ecuación auxiliar utilizada para Ecuaciones Diferenciales de 2º orden, siempre es:
| \begin{equation} {am}^2 + {bm} + c = 0 \end{equation} | (12) |
Donde la $ m$ es la que se sustituye en la $ {I}$ de la ecuación (10 u 11), aunque representan cosas distintas, ver el link.
Por tanto, desarrollando nuestro ejemplo, tenemos:
| \begin{eqnarray*} ( 0.1) {I}» + 50{I}’ + 2000{I} & \Rightarrow & 0.1 m^2 + 50 m^1 + 2000 m^0\\\\ & \Rightarrow & 0.1 m^2 + 50 m + 2000\\\\ & \Rightarrow & m^2 + 500 m + 20000\\\\ & \Rightarrow & ( m + 43.8447) ( m + 456.155) \end{eqnarray*} |
Por tanto las soluciones buscadas son:
| \begin{eqnarray*} m_1 & = & – 43.8447\\\\ m_2 & = & – 456.155 \end{eqnarray*} |
Esto implica que las funciones solución buscadas son:
| \begin{eqnarray*} {I}_1 & = & e^{- 43.8447 t}\\\\ {I}_2 & = & e^{- 456.155 t} \end{eqnarray*} |
Por el principio de superposición, que se aplica también a las soluciones encontradas de la Ecuación Homogénea (gracias a que estamos usando ecuaciones diferenciales lineales y homogéneas), sabemos que la combinación lineal de $ C_1 e^{- 43.8447 t} + C_2 e^{- 456.155 t}$ (ver el link del método para resolver Ecuaciones Lineales Homogéneas con Coeficientes Constantes), es una solución de la ecuación diferencial lineal y homogénea (9), y puesto que se deriva este resultado de la ecuación homogénea asociada, éste representa a la Corriente Transitoria, como lo mencionamos anteriormente, de modo que:
| \begin{equation} {I}_{{tr}} = C_1 e^{- 43.8447 t} + C_2 e^{- 456.155 t} \end{equation} | (13) |
Para encontrar los valores de $ C_{1}$ y $ C_{2}$, utilizamos los valores iniciales $ I(0)=0$ y $ Q(0)=0$, derivados del problema (donde se asume que en el tiempo $ 0$ el interruptor del problema está abierto por lo que no existe corriente y el capacitor no tiene carga) además como la ecuación (2) nos indica que:
$ \large LI^{‘}\left ( 0 \right )+RI\left ( 0 \right )+\frac{1}{C}Q\left ( 0 \right )=E\left ( 0 \right )$
Entonces asumimos que: $ I^{‘}\left ( 0 \right )=0$. Los valores para $ C_{1}$ y $ C_{2}$ se obtienen, de esta forma, después de haber obtenido el valor para la Corriente Periódica Estacionaria ($ I_{ps}$), la cual es el resultado de resolver el sistema no homogéneo con el siguiente método.
Ecuaciones Diferenciales lineales NO homogéneas con Coeficientes Indeterminados
Ahora, para encontrar la Corriente Periódica Estacionaria, utilizaremos el método de superposición para Ecuaciones Diferenciales con Coeficientes Indeterminados.
Este método asume que la segunda parte de la ecuación diferencial representa una solución particular del sistema no homogéneo al dividirla entre el coeficiente de la derivada de 2º orden. Esto decir, haciendo la analogía con la ecuación diferencial general de segundo orden
$ \Large {a}_2 y» +{a}_1 y’ +{a}_0 y = f ( x)$
y dividiendo entre el coeficiente de la derivada de 2º orden, se obtiene su forma Estándar:
$ \large y» + \frac{{a}_1}{{a}_2} y’ +\frac{{a}_0}{{a}_2} y = \frac{f ( x)}{{a}_2}$
la cual puede escribirse de forma mas compacta como:
| \begin{equation} y» +{b}y’ +{c}y = \frac{f ( x)}{{a}_2} \end{equation} | (14) |
La solución particular para ésta, sería:
| \begin{equation} y_p = \frac{f ( x)}{{a}_2} \end{equation} | (15) |
Sabemos, por el método utilizado (método de superposición para Ecuaciones Diferenciales con Coeficientes Indeterminados), que la una solución particular para nuestra ecuación diferencial se obtiene de utilizar (15), siempre y cuando $ f(x) = {constante}$, sin embargo, como en nuestro caso particular la función $ f(x)$ es de la forma:
$ \Large f ( x) = c A_{} \cos c x$
como lo muestra la fórmula (5), es necesario utilizar el siguiente criterio:
Como la solución particular buscada $ y_p$, (o mejor dicho en nuestro caso $ {I}_{{ps}}$) debe sustituirse en el primer miembro de la ecuación (7): $(0.1) {I}» + 50{I}’ + 2000{I}= ( 377) ( 110) \cos 377{t}$ y obtener como resultado su segundo miembro, la estrategia común es suponer que la función solución $ y_p$ (o $ {I}_{{ps}}$), tiene la forma del segundo miembro de la ecuación (7).
Escribiendo entonces la ecuación de nuestro ejemplo (7), y reduciendo términos en su segundo miembro, tenemos:
| \begin{eqnarray*} ( 0.1) {I}» + 50{I}’ + 2000{I} & = & 41470 \cos 377 t \end{eqnarray*} |
En este caso no dividimos el resultado entre el coeficiente $ {a}_2 =0.1$, pues como hemos comentado el valor de $ f(x) ( ={I} ( t))$, no es constante, de modo que nuestra ecuación diferencial a resolver es:
| \begin{equation} 0.1{I}» + 50{I}’ + 2000{I}= 41470 \cos 377 t \end{equation} | (16) |
De esta ecuación (16) y de la ecuación (15) vemos que $ f(x)$, es:
| \begin{eqnarray} f ( x) & = & {E} ( t) \nonumber\\ & = & {\omega}E_0 \cos {\omega}{t} \nonumber\\ & = & ( 377) ( 110) \cos 377{t} \nonumber\\ & = & 41470 \cos 377 t \end{eqnarray} | (17) |
Ahora, para obtener $ y_p ( ={I}_{{ps}})$, desarrollamos el método de los coeficientes indeterminados como sigue:
Podemos suponer que la solución particular $ {I}_{{ps}}$, es de la misma forma que la ecuación (17), es decir:
$ \Large {I}_{{ps}} = A \cos 377 t$
Donde:
$ A$: es un coeficiente constante indeterminado.
Sin embargo, como la ecuación diferencial (16), tiene las derivadas sucesivas $ {I}»$ e $ {I}’$ de $ {I}_{{ps}} = A \cos 377 t$ (ya que el sustituir estas derivadas de $ {I}_{{ps}}$ en la ecuación (16), nos pueda dar el resultado deseado), podemos asumir que la solución es de la forma:
| \begin{equation} {I}_{{ps}} = A \cos 377 t + B {sen} 377 t \end{equation} | (18) |
Donde:
$ A$ y $ B$: son coeficientes indeterminados constantes.
Ahora, procedemos a la sustitución de nuestra solución supuesta en la ecuación (16), para encontrar los coeficientes indeterminados, para eso, derivamos la solución propuesta (ecuación 18):
| \begin{equation} {I}’_{{ps}} ( t) = ( 377) B \cos 377 t – ( 377) A {sen} 377 t \end{equation} | (19) |
| \begin{equation} {I}»_{{ps}} ( t) = – 142129 A \cos 377 t – 142129 B {sen} 377 t \end{equation} | (20) |
Ahora sustituiremos estos resultados en la ecuación (16) y reduciremos términos:
| \begin{eqnarray} 0.1{I}» + 50{I}’ + 2000{I} & = & 41470 \cos 377 t \nonumber\\ 0.1 ( – 142129 A \cos 377 t – 142129 B {sen} 377 t) + 50 ( ( 377)\\ B \cos 377 t – ( 377) A {sen} 377 t) + 2000 ( A \cos 377 t + B {sen} 377 t) & = & 41470 \cos 377 t \nonumber\\ ( – 14212.9 A + 18850 B + 2000 A)\\ \cos 377 t + ( – 14212.9 B – 18850 A + 2000 B) {sen} 377 t & = & 41470 \cos 377 t \nonumber\\ ( – 12212.9 A + 18850 B) \cos 377 t + ( – 12212.9 B – 18850 A) {sen} 377 t & = & 41470 \cos 377 t \end{eqnarray} |
Ahora, para encontrar los coeficientes $ A$, $ B$, igualamos los términos del primer miembro de (21) con los términos del segundo miembro similares para formar un sistema de ecuaciones que nos permita despejar a $ A$ y a $ B$. Para esto utilizaremos el truco de agregar en el segundo miembro de (21) la función $ f(t) = {sen} 377 t$ pero multiplicada por $ 0$ (es decir $ f(t) = 0 {sen} 377 t$), para no alterar la ecuación, de manera que tenemos:
$ ( – 12212.9 A + 18850 B) \cos 377 t + ( – 12212.9 B – 18850 A) {sen} 377 t\\\\ = 41470 \cos 377 t + 0 {sen} 377 t$
De esta forma igualamos términos y formamos la ecuaciones:
| \begin{eqnarray*} – 12212.9 A + 18850 B & = & 41470\\\\ – 12212.9 B – 18850 A & = & 0 \end{eqnarray*} |
De donde:
| \begin{eqnarray*} A & = & – 1.00395\\\\ B & = & 1.54954 \end{eqnarray*} |
De modo que nuestra solución particular es:
| \begin{eqnarray} {I}_{{ps}} & = & A \cos 377 t + B {sen} 377 t \nonumber\\ & = & – 1.00395 \cos 377 t + 1.54954 {sen} 377 t \end{eqnarray} | (22) |
Ahora, como nuestra intensión es encontrar un resultado para $ I_{ps}$, que se asemeje al segundo miembro de la ecuación (16), utlilizaremos identidades trigonométricas para reducir nuestro resultado a la forma deseada.
Utlizamos, entonces, las siguiente identidades para un triángulo rectángulo:

| \begin{eqnarray*} C^2 & = & A^2 + B^2\\\\ \cos {\alpha} & = & \frac{A}{C}\\\\ \Rightarrow A & = & C \cos {\alpha}\\\\ {sen} {\alpha} & = & \frac{B}{C}\\\\ \Rightarrow B & = & C {sen} {\alpha}\\\\ \cos ( a – b) & = & \cos a \cos b + {sen} a {sen} b \end{eqnarray*} |
De este modo, para encontrar un valor para la ecuación (22) que se asemeje al segundo término de (16), hacemos lo siguiente:
| \begin{eqnarray*} A \cos {\omega}t + B {sen} {\omega}t & = & C \cos {\alpha} \cos {\omega}t + C {sen} {\alpha} {sen} {\omega}t \nonumber\\\\ & = & C ( \cos {\alpha} \cos {\omega}t + {sen} {\alpha} {sen} {\omega}t) \nonumber\\\\ & = & C ( \cos {\omega}t \cos {\alpha}+ {sen} {\omega}t {sen} {\alpha}) \nonumber\\\\ & = & C \cos ( {\omega}t – {\alpha}) \end{eqnarray*} | (23) |
Donde:
| \begin{equation} C = \sqrt{A^2 + B^2} \end{equation} | (24) |
Por lo que adecuando nuestro resultado a las ecuaciones (23) y (24), tenemos:
| \begin{eqnarray*} C & = & \sqrt{( – 1.00395)^2 + 1.54954^2}\\\\ & = & \sqrt{3.40899}\\\\ & = & 1.84635 \end{eqnarray*} |
Además, según la Figura 2:
| \begin{eqnarray*} \tan {\alpha} & = & \frac{B}{A}\\\\ \Rightarrow {\alpha} & = & \tan^{- 1} \frac{B}{A} \end{eqnarray*} |
De modo que:
| \begin{equation} {\alpha}= \tan^{- 1} \frac{1.54954}{1.00395} = 0.995899 \end{equation} | (25) |
Donde no hemos considerado el signo del valor de $ A$, pues ya lo hemos incluido en la ecuación (23)[Ver nota al final de la página].
De tal forma que la solución buscada es:
| \begin{equation} {I}_{{ps}} = 1.84635 \cos ( 377 t – 0.995899) \end{equation} | (26) |
La ecuación (26) proporciona la Corriente Periódica Estacionaria en función del coseno, mientras que el voltaje de entrada $ E ( t) = E_0 {sen} {\omega}t$, como una función seno, como lo muestra la ecuación (5) para el caso típico el voltaje de corriente alterna. Es por eso que puede ser conveniente (para manipular los resultados obtenidos en cálculos posteriores requeridos), convertir la ecuación (26) en una función seno.
Para esto volvemos a utilizar el Triángulo e Pitagoras y algunas identidades trigonométricas de la siguiente manera:

Figura 3. Triángulo de pitágoras con los ángulos $ \alpha$ y $ \delta$ señalados.
Utilizaremos las identidades, para relacionar ángulos complementarios de el mismo triángulo rectángulo de la Figura 3, de la siguiente manera:
| \begin{eqnarray*} C^2 & = & A^2 + B^2\\\\ \cos {\delta} & = & \frac{B}{C}\\\\ \Rightarrow B & = & C \cos {\delta}\\\\ {sen} {\delta} & = & \frac{A}{C}\\\\ \Rightarrow A & = & C {sen} {\delta}\\\\ {sen} ( a – b) & = & {sen} a \cos b – \cos a {sen} b \\\\ {sen} {\delta} & = & {sen} \left( {\alpha}- \frac{{\pi}}{2} \right) \end{eqnarray*} |
Las identidades trigonométricas $ \cos ( a – b)$ y $ {sen} ( a – b)$, que aquí utilizamos, utilizan a su vez los ángulos internos de un mismo triángulo rectángulo, el de la Figura 4, donde $ {\delta}={\alpha}- \frac{{\pi}}{2}$, (Ver nota al final de la página)
De modo que, recalculando los valores para nuestra ecuación (22) para que se asemeje a la ecuación (5), tenemos:
| \begin{eqnarray} A \cos {\omega}t + B {sen} {\omega}t & = & C {sen} {\delta} \cos {\omega}t – C \cos {\delta} {sen} {\omega}t \nonumber\\\\ & = & C ( {sen} {\delta} \cos {\omega}t – \cos {\delta} {sen} {\omega}t) \nonumber\\\\ & = & C {sen} ( {\omega}t -{\delta}) \end{eqnarray} | (27) |
Donde:
$ \Large \tan {\delta}= \frac{A}{B} = \frac{1.00395}{1.54954} \Rightarrow \delta = 0.574897$
Utilizando los mismos coeficientes $ A$, $ B$, encontrados previamente, según la Figura 4. No hemos considerado el signo del valor de $ A$, pues ya lo hemos incluido en la ecuación (31)[Ver nota al final de la página].
Por lo que la solución buscada utilizando el resultado (27) y el valor de $ C$ previamente obtenido, es:
$ \Large {I}_{{ps}} = 1.84635 {sen} ( 377 t – 0.574897)$
Puesto que $ C$ tiene el mismo valor de antes.
Importante: utilizar radianes no grados para el cálgulo de los angulos $ \alpha$ y $ \delta$
NOTA:
Es importante mencionar que la elección de las identidades trigonométricas tienen un criterio incluido. Este criterio obedece al comportamiento que tiene la corriente con respecto del voltaje al desplazarse en el tiempo; es decir, si vemos la Figura 3, notaremos que el voltaje y la corriente, tienen un defasamiento entre sí cuando se propagan en el tiempo.
Este defasamiento es igual al ángulo $ {\delta}$ el cual, relacionándolo con $ {\alpha}$, es igual a:
$ \Large {\delta}={\alpha}- \frac{{\pi}}{2}$
y representa un retraso de la corriente $ I_{{ps}} ( t)$ con respecto del Voltaje $ E(t)$, como se ve en la Figura 3.

Figura 4. Ángulo de defasamiento $ \delta =\alpha -\frac{\pi }{2}$ que representa el atraso de la corriente $ I_{ps}$ con respecto del Voltaje de suministro del circuito RLC, $ E(t)$.
Para nuestro caso particular los valores de $ {\delta}$ y $ {\alpha}$, se muestran en la ecuación (26) y en la Figura 4, como:
| \begin{eqnarray*} {\alpha} & = & 0.995899\\\\ {\delta} & = & {\alpha}- \frac{{\pi}}{2}\\\\ & = & 0.995899 – 1.570796\\\\ & = & – 0.574897 \end{eqnarray*} |
El resultado final no incluye los valores de $ C_{1}$ y $ C_{2}$. Para conocer cómo obtener estos valores ve el artículo: Programa para Simular Circuitos Electricos con MATHEMATICA
Para simular el comportamiento de este circuito RLC en MATHEMATICA utiliza el siguiente código: da click aquí
Circuito electrico mixto

Ecuaciones Diferenciales Aplicaciones
Desarrollar tu intuición y confía en ella cuando estés estudiando ecuaciones diferenciales. Para esto necesitas preparar tu mente, por eso te invito a leer el artículo La técnica perfecta para aprender ecuaciones diferenciales, da click aquí, y practicar con varios ejercicios, de manera que luego, al estudiar los conceptos a fondo tengas toda la información necesaria y verás como todo se aclara, pues tu mente entenderá con facilidad los conceptos más abstractos.
Quiero un ejemplo para un sistema de primer orden RL (Click aquí)
Quiero un ejemplo para un sistema de primer orden RC (Click aquí)
Encontraste la información que buscabas?
Te invito a que me contactes aquí para cualquier sugerencia sobre la página y si tienes una duda en particular sobre el tema tratado, por favor, deja tu comentario al final de esta página. Que estés bien. 😉

Realmente se nota el esfuerzo y el empeño que pusiste en la realización de la página. Lamentablemente no se Nada de Ecuaciones Diferenciales, pero estoy seguro que con tu aporte lo lograre. Muchas gracias y felicidades por tan buen Blog.
No habra mayor recompensa que el saber que contribuí a tu propósito Ruben, te agradezco el comentario. Te pido por favor que en tu estudio de la materia me hagas saber todo en lo que te pueda ayudar, por favor. Un saludo y por aquí nos vemos. AVR
Me parece fabulosa la página, felicitaciones.
Excelente trabajo. Referiré tu pagina a mis estudiantes de análisis de circuitos, para que usen tu aportación como herramienta de ayuda.
Julio, te agradezco muchísimo tu comentario es un empujon de energía sinceramente. Me da mucho gusto que sea de utilidad para tí y para tus alumnos mi trabajo y me sirve mucho para seguir con esta labor. Dicho sea de paso he pensado en preparar material para análisis de circuito eléctricos (individuales y sistemas) con laplace porque es un área que me facina y la tengo pendiente, si tienes alguna sugerencia de qué debo incluir, te agradecería mucho me la hicieras llegar. Te dejo mi correo: ecuaciondiferencialavr@gmail.com. De nuevo gracias y si en algo más te puedo apoyar no dudes en avisarme. Saludos
Está página es fantástica, realmente. Gracias por tus aportes.
Muchas gracias Lionel, por tu comentario. Es muy motivador escuchar que te ha parecido fantástica. ¿Nos ayudas a difundirla? te dejo un enlace a nuestra página de facebook: Ecuaciones Diferenciales Ejercicios y aplicaciones
Gracias de nuevo por tu comentario y que estes muy bien. Un saludo
como podría cerrar con alguna conclusión, me ayudas por favor
No entiendo a qué te refieres Arturo. ¿Conclusión de que perdón? ¿Podrías precisar más? Un saludo