Función dividida en partes y su Continuidad 

En ocasiones encontraremos funciones de entrada divididas en partes para una Ecuación diferencial, en estos casos para encontrar una solución particular de la ED, si se conocen los valores iniciales, será necesario considerar que dicha solución será, de igual manera, una función dividida en partes y que para encontrar las soluciones particulares de cada una de sus partes será necesario el uso del concepto de continuidad.

Desarrollemos un ejemplo para cubrir este tema. Tenemos la EDO lineal de orden 1:

$$ \frac{dy}{dx}+2xy=f(x)$$$$ y\left( 0 \right)=2$$

(1)

Con $f(x)$ dividida en partes:

$$f(x)=\left\{\begin{matrix}x,0\leq x< 1\\ 0,x\geq 1\end{matrix}\right.$$

Al buscar su función solución PARTICULAR nos toparemos con dos casos:

• Una función solución para cuando la función de entrada es igual a: $f(x)=x$
• Otra función solución para cuando la función de entrada es igual a: $f(x)=0$

Para el primer caso no tendremos problema de encontrar la solución particular utilizando los valores iniciales $y\left( 0 \right)=2$, ya que la restricción ($0\leq x< 1$) para ese caso nos permite utilizar dichos valores. Sin embargo, para el segundo caso no podemos considerar sustituir $x=0$, en la solución general obtenida para cuando $f(x)=0$:

$${{y}_{2}}\left( x \right)=\frac{C}{{{e}^{{{x}^{2}}}}}$$

Ya que:

$$x\ge 1$$

ver cálculo de la Solución General para éste Ecuación diferencial (1) en el siguiente link (click aquí), Por tanto, recurriremos al concepto de CONTINUIDAD.

TEOREMA

Continuidad: “El límite de una función cuando su variable independiente tiende a un número específico, existe, si el límite de la función, cuando tiende a ese número por la derecha es igual al límite cuando la función tiende a ese número por la izquierda”.

Es decir, para este caso:

$\underset{x\to {{1}^{-}}}{\mathop{\lim }}\,y(x)=\underset{x\to {{1}^{+}}}{\mathop{\lim }}\,y(x)\to \exists \underset{x\to 1}{\mathop{\lim }}\,y(x)$.

Donde:  $\exists =$ Existe

Con este teorema encontraremos el valor de “C”, para hallar la Respuesta del Sistema cuando la función de entrada es: $\text{f}\left( \text{x} \right)=0$, suponiendo que el límite existe.

Entonces, el límite por la izquierda:

$\underset{x\to {{1}^{-}}}{\mathop{\lim }}\,y(x)=\underset{x\to 1}{\mathop{\lim }}\,\frac{3}{2{{e}^{{{x}^{2}}}}}+\frac{1}{2}=\frac{3}{2{{e}^{{{(1)}^{2}}}}}+\frac{1}{2}=\frac{3}{2\text{e}}+\frac{1}{2}$, cuando:  $0\le x<1$

Y el límite por la derecha:

$\underset{x\to {{1}^{+}}}{\mathop{\lim }}\,y(x)=\underset{x\to 1}{\mathop{\lim }}\,\frac{C}{{{e}^{{{x}^{2}}}}}=\frac{C}{{{e}^{{{(1)}^{2}}}}}=\frac{C}{\text{e}}$, cuando:  $x\ge 1$

Por tanto, con la suposición de que el límite existe, igualamos los resultados anteriores:

$\frac{3}{2\text{e}}+\frac{1}{2}=\frac{C}{\text{e}}$

Esto implica:

$C=\frac{3}{2}+\frac{e}{2}$, Por último:

${{y}_{2}}\left( x \right)=\frac{C}{{{e}^{{{x}^{2}}}}}=\frac{\frac{3}{2}+\frac{e}{2}}{{{e}^{{{x}^{2}}}}}=\frac{3{{e}^{-{{x}^{2}}}}}{2}+\frac{{{e}^{1-{{x}^{2}}}}}{2}$

De esta forma, la solución del Sistema Lineal, dividida en partes, con valores iniciales, es:

$\LARGE f(x)=\left\{\begin{matrix}\frac{3}{2e^{x^{2}}}+\frac{1}{2},0\leq x< 1\\ \frac{3e^{-x^{2}}}{2}+\frac{e^{1-x^{2}}}{2},x\geq 1\end{matrix}\right.$

Este resultado es válido, aparentemente al haber empleado la definición de Continuidad, sin embargo, habrá que verificarlo y lo haremos y veremos que no es válido el resultado por la definición de SOLUCIÓN DE UNA ED EN UN INTERVALO, que dice que la solución de una ED diferencial y sus derivadas al sustituirlas en esta, la reducen a una identidad.

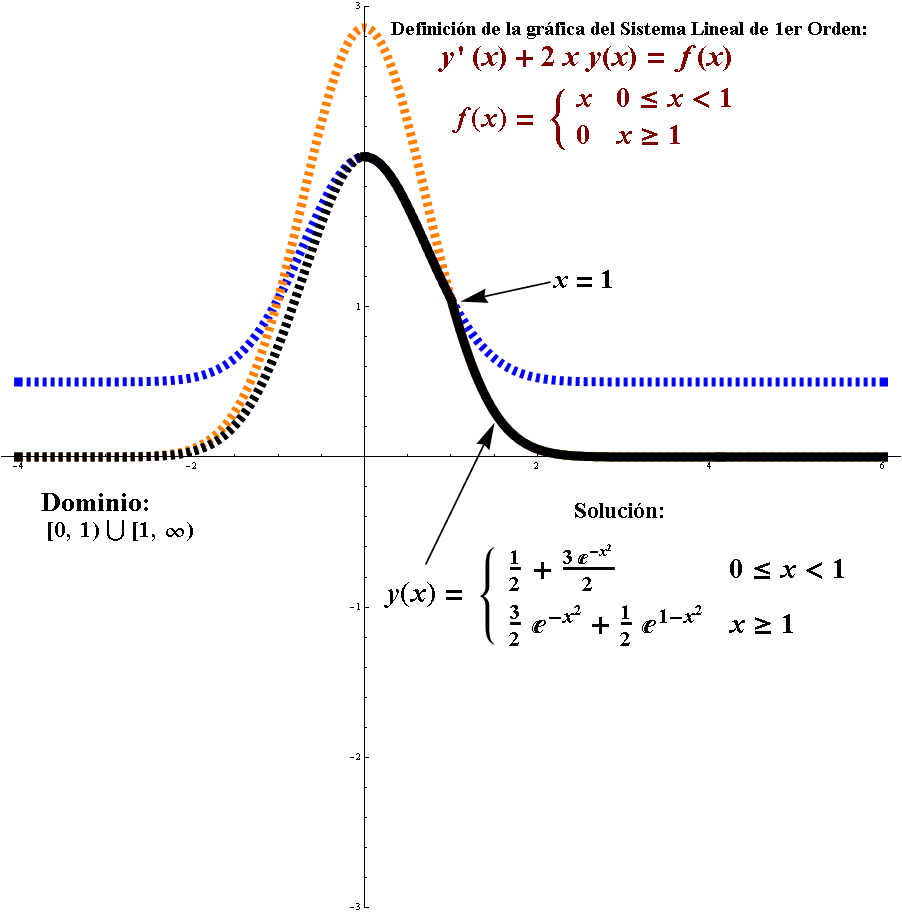
Para nuestro caso, la definición de «Solución de una ED en un intervalo «, no se cumple, puesto que para un mismo punto (punto $x=1$ ), tenemos dos funciones, como lo evidencia la siguiente Figura.       Ahora aplicando la definición de «Solución de una ED en un intervalo», tenemos: Derivando el lado derecho de la función de salida y el lado izquierdo.

${{y}_{1}}\left( x \right)=\frac{3}{2{{e}^{{{x}^{2}}}}}+\frac{1}{2}$

$\Rightarrow y_{1}’\left( x \right)=\frac{3}{2}{{e}^{-{{x}^{2}}}}\left( -2x \right)+0$   $\Rightarrow y_{1}’\left( x \right)=-3x{{e}^{-{{x}^{2}}}}$

y

${{y}_{2}}\left( x \right)=\frac{3{{e}^{-{{x}^{2}}}}}{2}+\frac{{{e}^{1-{{x}^{2}}}}}{2}$

$\Rightarrow y_{2}’\left( x \right)=\frac{3}{2}{{e}^{-{{x}^{2}}}}\left( -2x \right)+\frac{1}{2}{{e}^{1-{{x}^{2}}}}\left( -2x \right)$   $\Rightarrow y_{2}’\left( x \right)=-3x{{e}^{-{{x}^{2}}}}-x{{e}^{1-{{x}^{2}}}}$

E igualando los resultados, tenemos:

$\Rightarrow -3x{{e}^{-{{x}^{2}}}}=-3x{{e}^{-{{x}^{2}}}}-x{{e}^{1-{{x}^{2}}}}$

$\Rightarrow 0=-x{{e}^{1-{{x}^{2}}}}$

Por lo que al no obtener una identidad, la ecuación no es diferenciable en $x=1$.

Ecuaciones Diferenciales

Programa Completo

Apúntate a nuestro PROGRAMA COMPLETO de Ecuaciones Diferenciales y conviertete en lo que ERES. Aduéñate de todos los proyectos!!!

Dale click al siguiente enlace e inscríbete YA!!!

Ecuaciones Diferenciales Programa Completo, click aquí

Para que obtengas la confianza necesaria en tu vida PROFESIONAL y en tu persona realiza ejercicios de aplicación y practica

En nuestro Programa Completo de Ecuaciones Diferenciales, aprenderás:

• Realizar Modelado Matemático
• Aplicar los algoritmos de solución. Te enseñamos a saber:
  • ¿Por donde Empezar cuando tengo una ED enfrente?
  • ¿Qué tipo de Ecuacion Diferencial tengo enfrente?
  • ¿Qué método emplear para resolve la ED que tengo enfrente?
• Realizar simulación por computadora (simbólica y numérica) para transformar tu realidad y la de tu entorno, brindando servicio efectivo y sintiendote realizado como ingeniero, como matemñatico aplicado
• Inscríbete a nuestro PROGRAMA COMPLETO de ECUACIONES DIFERENCIALES

Aplicaciones de las Ecuaciones Diferenciales

Practica los ejercicios utilizando la técnica adecuada, para esto te invito a que revises la técnica que te describo en el siguiente link: La Técnica Perfecta para Aprender Ecuaciones Diferenciales y te dediques diariamente a resolver al menos un ejercicio aplicando la técnica que te describo, además de los problemas de tarea que tengas al comienzo de tu estudio de esta fascinante materia.

Ver mas ejemplos?  

probl 32, problema 34, probl 35

Quiero saber como expresar mi resultado usando la Función Error (Dale Click aquí)

Quiero aprender a simular mis Ecuaciones Diferenciales con un Software de Computadora (Dale Click)

Te ha servido el artículo? contáctame para cualquier sugerencia o duda en el siguiente link: contacto Mientras te dejo con mi artículo: La técnica perfecta para aprender ecuaciones diferenciales. Seguramente te facilitará tus estudios y te hará mas fácil la vida. 😉