Ecuaciones Diferenciales de Lagrange Ejercicios Resueltos

Sección	Resumen
1. Motivación para estudiar	Después de terminar de leer este artículo, podrás tener una idea clara de cómo abordar problemas de ecuaciones diferenciales de Lagrange cuando pueden ser reducidas a la forma estándar $y=xf(y’)+g(y’)$, utilizando una metodología que te ayude a resolverlas.
2. Lagrange detrás de la Máscara	La Verdadera Historia de Joseph-Louis Lagrange.
3. Aplicaciones de la ED de Lagrange	Descubre que tan poderoso es aprender las ecuaciones de lagrange tomando en cuenta su gran variedad de su campo de aplicación. Ejemplos de aplicaciones.
4. Metodología	Metodología de 6 pasos para resolver la ecuación de lagrange de primer orden: $y=xf(y’)+g(y’)$
5. Ejercicios resueltos paso a paso	Ejercicios resueltos paso a paso y a detalle, desarrollando la metodología mencionada, para que internalices el método de manera definitiva.
6. Conviertete en un Expert@	Desbloquea tu potencial y alcanza la maestría en Ecuaciones Diferenciales e Inteligencia Artificial

Motivación para estudiar

Si lees ecuaciones diferenciales de Lagrange ejercicios resueltos, hasta el final del artículo, dominarás los conceptos clave y metodologías necesarias para abordar estos problemas, superando la percepción de dificultad y encontrando aplicaciones prácticas.

¿Te frustran las ecuaciones diferenciales de Lagrange? ¿Sientes que son demasiado complejas y difíciles de aprender? ¿Te gustaría tener una metodología clara y sencilla para resolverlas?

En éste artículo responderesmos a tus preguntas.

Las ecuaciones de Lagrange son a menudo percibidas como un tema complejo y desafiante, lo que puede desanimar a algunos estudiantes y docentes. Sin embargo, al comprender y aplicar de manera efectiva los algoritmos de solución presentados aquí, podrás abordar estas ecuaciones con confianza y éxito.

Además, este artículo proporciona ejemplos concretos de aplicaciones de las ecuaciones de Lagrange en el mundo real, lo que te ayudará a ver su relevancia y utilidad en diversos contextos.

Al final de éste artículo, serás capaz de:

• Identificar si una ecuación diferencial es de Lagrange.
• Aplicar la metodología para resolver ED de Lagrange no-lineales.
• Interpretar los resultados de la solución.

Observa tus pensamientos, porque se convierten en palabras. Observa tus palabras, porque se convierten en acciones. Observa tus acciones, porque se convierten en hábitos. Observa tus hábitos, porque se convierten en tu carácter. Observa tu carácter, porque determina tu destino.

Dhammapada (Budismo)

Lagrange detrás de la máscara.

Joseph-Louis Lagrange, también conocido como Giuseppe Lodovico Lagrangia, fue un matemático, físico y astrónomo italiano. Nació el 25 de enero de 1736 en Turín, Reino de Cerdeña, y pasó la mayor parte de su vida en Prusia y Francia.

Lagrange procedía de una familia parisina que gozaba de buena posición social. Fue el mayor de once hermanos y el único que alcanzó la edad adulta. Fue educado en la Universidad de Turín y no fue hasta los diecisiete años cuando mostró interés por la matemática. Su entusiasmo empezó a caminar con la lectura de un ensayo del astrónomo Edmund Halley sobre análisis matemático. Tras un año de incesante trabajo, era ya un matemático consumado.

En 1761 Lagrange no tenía rival en el campo de las matemáticas; pero su trabajo incesante durante los últimos nueve años había afectado seriamente a su salud, y los doctores se negaron a ser responsables de su vida a menos que él se lo tomara en serio. Aunque su salud fue temporalmente restablecida, su sistema nervioso nunca recuperó su tono y de aquí en adelante padeció constantemente ataques de melancolía severa.

En 1766, tras la invitación de Federico ll el Grande y vivio 20 años de su vida en Prusia. Lagrange era el favorito del rey y frecuentemente disertó sobre las ventajas de una regularidad perfecta en la vida. La lección la aplicó a su propia vida: estudió su mente y su cuerpo como si fueran máquinas, y encontró experimentando la cantidad exacta de trabajo que podía hacer sin perder la salud.

En 1775 fue nombrado profesor de la Escuela de Artillería y fundó una sociedad matemática en Turín. Resultó ser un profesor problemático por su estilo dominado por el razonamiento abstracto; dispuesto a relegar a un segundo plano la práctica de la artillería y de la ingeniería de las fortificaciones.

En cuanto a su vida y costumbres, todas las noches se ponía una tarea definida para el día siguiente, y al completar cualquier tema escribía un corto análisis para ver qué puntos en las demostraciones eran susceptibles de mejora. Siempre pensó en sus artículos antes de componerlos, y normalmente los escribió con esmero y sin una sola raspadura o corrección.

Pese a las adversidades de salud y familiares, puesto que su padre, perdío su fortuna en especulaciones, siendo tesorero del reino de Sardania, Lagrange realizó grandes contribuciones a un amplio rango de la matemáticas, incluyendo las ecuaciones diferenciales. Una vez dijo:

Si hubiera sido rico, probablemente no habría sido devoto de las matemáticas

Joseph-Louis Lagrange

Lagrange era de mediana estatura, complexión débil, con ojos azul claro y un color de piel pálido. Era de un carácter nervioso y tímido, detestó la controversia, y al evitarla de buena gana permitió a otros tener crédito por cosas que él había hecho. Contribuyó significativamente a multiples y diversas áreas de las matemáticas y la física, siendo su mas grande obra: Mecanique analytique, 1788.

Además contribuyo en áreas como:

Cálculo de variaciones

• Fue uno de los creadores del cálculo de variaciones.
• Derivó las ecuaciones de Euler-Lagrange para encontrar extremos de funcionales.
• Extendió el método para incluir posibles restricciones, llegando al método de los multiplicadores de Lagrange.

Ecuaciones diferenciales de Lagrange

1. Lagrange inventó el método de solución de ecuaciones diferenciales conocido como variación de parámetros. Por este método y por sus numerosas aportaciones se le considera uno los mayores matemáticos de todos los tiempos
2. La ecuación $y=xf'(y’)+g(y’)$ lleva su nombre y es fundamental en la teoría de ecuaciones diferenciales.

Otros campos de la matemática influidos por Lagrange

Lagrange hizo importantes avances en álgebra, incluyendo el desarrollo de métodos para resolver ecuaciones algebraicas. Lagrange realizó contribuciones significativas en teoría de números. Demostró que todo número natural es la suma de cuatro cuadrados.

Su tratado Théorie des fonctions analytiques, sobre funciones analíticas, contribuyó al desarrollo de la teoría de grupos, anticipando a Galois.

Lagrange trabajó en fracciones continuas, un área matemática que involucra representaciones aproximadas de números racionales.

Lagrange no formuló ecuaciones específicas en este campo, pero su trabajo en cálculo de variaciones y mecánica analítica influyó en la resolución de ecuaciones diferenciales.

Joseph-Louis Lagrange, muere en abril de 1813 a la edad de 77 años.
Inspirado por su perseverancia y logros, recordamos a Lagrange como un ejemplo de superación y dedicación en el mundo de las matemáticas y la ciencia.

Aplicaciones de las Ecuaciones Diferenciales de Lagrange Ejercicios Resueltos.

Los intereses de Lagrange eran esencialmente aquellos de un estudiante de matemática pura: buscó y obtuvo resultados abstractos de largo alcance, y estaba satisfecho de dejar las aplicaciones a otros. De hecho parte de los descubrimientos de su gran contemporáneo, Laplace, consiste en la aplicación de las fórmulas de Lagrange a los fenómenos de la naturaleza; por ejemplo, las conclusiones de Laplace de la velocidad del sonido y de la aceleración secular de la Luna están ya implícitamente en los resultados de Lagrange.

Problemas de Dinámica y Gravitación.

En sistemas de tres cuerpos, como el problema de los planetas en órbita, las ecuaciones de Lagrange permiten describir las trayectorias y las interacciones gravitatorias.

Teoría de Propagación del sonido.

En sistemas de tres cuerpos, como el problema de los planetas en órbita, las ecuaciones de Lagrange permiten describir las trayectorias y las interacciones gravitatorias.

En cuanto a la propagación del sonido, Lagrange llegó a la conclusión de que la forma de la curva para un tiempo t cualquiera viene dada por la ecuación:

$$y=a\sin{(mt)}\sin{nt}$$

Cálculo de Variaciones y Principio de Mínima Acción.

El principio de mínima acción es fundamental en la física y se basa en el trabajo de Lagrange.

La idea central es que la trayectoria real de un sistema físico entre dos puntos en el espacio-tiempo es aquella que minimiza la acción (la integral del lagrangiano a lo largo de la trayectoria).

Aplicaciones de la Ecuación de Lagrange: $y=xf(y’)+g(y’)$

La ecuación aparece en el contexto de la teoría de funciones analíticas. Se utiliza para modelar funciones que son analíticas en un dominio específico. También aparece aparece en la resolución de multiples problemas de dinámica, por ejemplo, puede describir el movimiento de tres cuerpos mutuamente atraídos por la gravedad.

Un ejemplo de su aparición en problemas como la tensión del pendulo simple, se dá a continuación:

$$\lambda = -ml\dot{\theta}^{2}-mg\cos{\theta}$$

Metodología

La metodología presentada consta de 6 pasos concretos. A continuación se detallan dichos pasos para resolver la ED de Lagrange:

Paso 1. Escribimos la forma estándar de la ED y definimos si es un ED de Lagrange:

$$y=xf(y’)+g(y’)$$

Se comienza identificando la forma estándar de la ecuación diferencial y determinando si se puede reducir a una forma de Lagrange.

Paso 2. Sustituimos $y’=p$, donde $p=p(x)$, para encontrar la solución general den forma paramétrica transformando la ED a una ED de terminos algebraicos más manejables:

$$y=xf(p)+g(p)$$

Paso 3. Derivamos respecto de $x$ y despejamos $\frac{dp}{dx}$:

\begin{eqnarray*} \frac{d y}{d x} & = & x f’ (p) p’ + f (p) + g’ (p) p’\\ \frac{d y}{d x} & = & (x f’ (p) + g’ (p)) p’ + f (p)\\ (xf’ (p) + g (p)) p’ & = & \frac{d y}{d x} – f (p) \end{eqnarray*}

Sustituimos, $\frac{dy}{dx}=p$:

\begin{eqnarray*} p’ & = & \frac{p – f (p)}{x f’ (p) + g’ (p)}\\ \frac{d p}{d x} & = & \frac{p – f (p)}{x f’ (p) + g’ (p)} \end{eqnarray*}

Notar que la ED anterior es lineal para $x$ (ésto siempre sucede así). De modo que:

$$\frac{dx}{dp}=\frac{xf'(p)+g'(p)}{p-f(p)}$$

Paso 4. Resolvemos la ED lineal:

$$\frac{d x}{d p} = \frac{f’ (p)}{p – f (p)} x + \frac{g’ (p)}{p – f (p)}$$

Se resuelve la ecuación lineal obtenida en el paso anterior para encontrar una solución general.

Paso 5. Soluciones param{etricas. De la resoluci{on de la ED lineal, obtenemos:

$$x=h(p,C)$$

Sustituimos éste resueltado en la ED original, y obtenemos.

$$y=h(p,C)f(p)+g(p)$$

De modo que las soluciones paramétricas son:

\begin{eqnarray*} x & = & h (p, C)\\ y & = & h (p, C) f (p) + g (p) \end{eqnarray*}

Se utiliza la solución de la ecuación diferencial lineal para obtener las soluciones paramétricas finales. Éste paso es solo si no se puede encontrar una solución $y=f(x,C)$.

Paso 6. Soluciones singulares. Básicamente buscamos eliminar el parámetro p en la ecuación y y obtener una sulución de la forma:

$$F(x,y)=0$$

Podemos aplicar el jacobiano,

$$\det \left(\begin{array}{cc} X_c & Y_c\\ X_p & Y_p \end{array}\right) = 0$$

Y despejar

$$C=C(p)$$

para despues sustituir estos resultados en las soluciones paramétricas y así eliminar el parámero p en la ecuación $y$.

Tambien podemos buscar singularidades en las soluciones paramétricas como por ejemplo, si tenemos: $l n(p-1)$ como uno de los términos, podemos notar que si $p=1$, se forma una singularidad que podemos sustituir en $y$ para obtener la solución singular.

Esta metodología proporciona un marco claro y efectivo para abordar problemas de ecuaciones diferenciales de Lagrange, lo que permite a los estudiantes y profesionales comprender y resolver estos problemas con mayor facilidad y precisión.

Si quieres automatizar tus soluciones con programación, utilizando un programa potente y fácil de aprender como sagemath, te recomendamos nuestra: Calculadora de ecuaciones diferenciales lagrange (codigo), para que estes seguro de tus soluciones, no pierdas tiempo y puedas hacer simulación.

Ecuaciones Diferenciales de Lagrange Ejercicios Resueltos

---

Ejercicio 1.

Resolver:

$$y = x + y’ – 3 (y’)$$

Solución.

Paso 1. Sustituimos $y’=p$.

$$y=x+p-3p^{2} …(1)$$

Paso 2. Derivamos respecto de $x$.

$$\frac{dy}{dx}=1+p’-6pp’$$

Paso 3. Despejamos para $x$.

Si $y’=p$, entonces:

\begin{eqnarray*} p & = & 1 + p’ – 6 p p’\\ p & = & 1 + (1 – 6 p) p’\\ (1 – 6 p) p’ & = & p – 1\\ \frac{d p}{d x} & = & \frac{p – 1}{1 – 6 p}\\ \frac{1 – 6 p}{p – 1} d p & = & d x \end{eqnarray*}

Paso 4. Resolvemos la ED lineal. (En éste caso particular la ED es separable, simplemente)

$$\int{\frac{dp}{p-1}}-6\int{\frac{pdp}{p-1}}=\int{dx+C}$$

Para integrar el segundo término del miembro izquierdo, utilizamos fracciones parciales.

$$\frac{p}{p-1}=1+\frac{1}{p-1}$$

Éste resultado se obtiene dividiendo $p$ entre $p-1$. De modo que:

\begin{eqnarray*} \int \frac{d p}{p – 1} – 6 \int \frac{p d p}{p – 1} & = & \int d x + C\\ l n (p – 1) – 6 \left[ \int d p + \int \frac{d p}{p – 1} \right] & = & \int d x + C\\ l n (p – 1) – 6 l n (p – 1) – 6 p & = & x + C\\ – 5 l n (p – 1) – 6 p & = & x + l n (C)\\ x & = & – 5 l n (p – 1) – 6 p – l n (C) \end{eqnarray*}

Paso 5. Soluciones paramétricas.

Sustituimos en (1), el resultado anterior:

\begin{eqnarray*} y & = & x + p – 3 p^2\\ y & = & (- 5 l n (p – 1) – 6 p – l n (C)) + p – 3 p^2 \end{eqnarray*}

Es decir, las ecuaciones paramétricas son:

\begin{eqnarray*} x & = & – 5 l n (p – 1) – 6 p – l n (C)\\ y & = & (- 5 l n (p – 1) – 6 p – l n (C)) + p – 3 p^2 \end{eqnarray*}

Paso 6. Solucion(es) singular(es)

Podemos considerar que una solución no contemplada al variar los parámetros se da cuando $p=1$, por tanto, si $p=1$, entonces:

\begin{eqnarray*} y & = & x + p – 3 p^2\\ y & = & x + 1 – 3\\ y & = & x – 2 \end{eqnarray*}

La solución singular buscada es:

$$y=x-2$$

---

Ejercicio 2.

Resolver:

$$y=2xy’-(y’)^{2}$$

Solución.

Paso 1. Sustituimos $y=p’$.

$$y=2xp-p^{2}…(2)$$

Paso 2. Derivamos respecto de $x$.

$$\frac{dy}{dx}=2p+2xp’-2pp’$$

Paso 3. Despejamos para $x$.

si $y’=p$, entonces:

\begin{eqnarray*} p & = & 2 (x – p) p’ + 2 p\\ p – 2 p & = & 2 (x – p) p’\\ – p & = & 2 (x – p) p’\\ 2 (x – p) p’ & = & – p\\ \frac{d p}{d x} & = & \frac{- p}{2 (x – p)} \end{eqnarray*}

La ED anterior es lineal en $x$, por tanto:

\begin{eqnarray} \frac{d x}{d p} & = & – \frac{2 (x – p)}{p} \nonumber\\ \frac{d x}{d p} & = & – \frac{2}{p} x + 2 \nonumber\\ \frac{d x}{d p} + \frac{2}{p} x & = & 2 …(3) \end{eqnarray}

Paso 4. Resolvemos la ED lineal.

Calculamos el factor integrante:

\begin{eqnarray*} {e^{\int P (p) d p}} & \Rightarrow & P (p) d p = \frac{2}{p} d p\\ & \Rightarrow & \int P (p) d p = 2 \int \frac{d p}{p}\\ & \Rightarrow & \int P (p) d p = 2 l n (p) \end{eqnarray*}

Por tanto:

$$e^{l n (p)^2} = p^2$$

De modo que, multiplicando el factor integrante por la ED (3) original:

\begin{eqnarray*} p^2 \left( \frac{d x}{d p} + \frac{2}{p} x \right) & = & 2 p^2\\ p^2 \frac{d x}{d p} + 2 p x & = & 2 p^2\\ \frac{d}{d x} (p^2 x) & = & 2 p^2\\ d (p^2 x) & = & 2 p^2 d x \end{eqnarray*}

Integrando:

\begin{eqnarray*} \int d (p^2 x) d p & = & 2 \int p^2 d x + C\\ x p^2 & = & \frac{2}{3} p^3 + C\\ x & = & \frac{2}{3} p + C p^{- 2} \end{eqnarray*}

Paso 5. Soluciones paramétricas

Sustituyendo en (2) el resultado anterior:

\begin{eqnarray*} y & = & 2 x p – p^2\\ y & = & 2 \left( \frac{2}{3} p + C p^{- 2} \right) p – p^2\\ y & = & \frac{4}{3} p + 2 C p^{- 2} – p^2 \end{eqnarray*}

De modo que, las ecuaciones paramétricas son:

\begin{eqnarray*} x & = & \frac{2}{3} p + \frac{C}{p^2}\\ y & = & \left( \frac{4}{3} p + 2 \frac{C}{p^2} \right) p – p^2 \end{eqnarray*}

Desarrollando obtenemos:

\begin{eqnarray*} x & = & \frac{2}{3} p + \frac{C}{p^2}\\ y & = & \frac{1}{3} p^2 + 2 \frac{C}{p} \end{eqnarray*}

Paso 6. Soluciones Singulares.

Utilizamos el determinante de la matriz jacobiana igualada a $0$, para despejar $C=C(p)$ y sustituir los resultados en las euaciones parametricas para obtner la envolvente (o solución singular).

\begin{eqnarray*} \det \left( \begin{array}{cc} X_c & Y_c\\ X_p & Y_p \end{array} \right) & = & 0\\ \det \left( \begin{array}{cc} \frac{1}{p^2} & \frac{2}{p}\\ – \frac{2 C}{p^3} + \frac{2}{3} & \frac{2}{3} p – \frac{2 C}{p^2} \end{array} \right) & = & 0\\ \frac{4 \left( \frac{3 C}{p^3} – 1 \right)}{3 p} + \frac{2 \left( p – \frac{3 C}{p^2} \right)}{3 p^2} & = & 0 \end{eqnarray*}

Y resolviendo para C, tenemos:

$$C=\frac{1}{3}p^{3}$$

Ahora, sustituyendo en las ecuaciones paramétricas, obtenemos:

\begin{eqnarray*} x & = & p\\ y & = & p^2 \end{eqnarray*}

Con el cual podemos graficar o tambien podemos sustituir el valor de $p$ la ecuación (2), de donde:

\begin{eqnarray*} y & = & 2 x x – x^2\\ y & = & 2 x^2 – x^2\\ y & = & x^2 \end{eqnarray*}

Siendo la envolvente o solución singular:

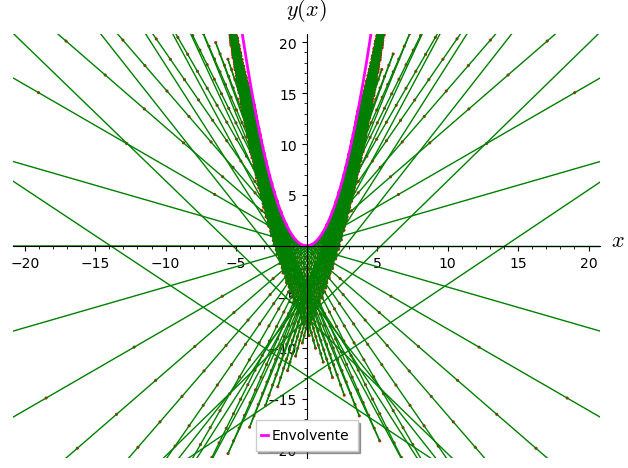
$$y=x^{2}$$

Grafica de la envolvente.

La gráfica de la envolvente junto con las rectas es:

---

Ejercicio 3.

Resolver:

$$y=\left(\cos{(y’)}+y’\right)x+\frac{1}{2}\sin{(y’)}\cos{(y’)}+\frac{1}{2}y’$$

Solución

Paso 1. Sustituimos $y’=p$.

\begin{equation} y = (\cos (p) + p) x + \frac{1}{2} \sin (p) \cos (p) + \frac{1}{2} p …4 \end{equation}

paso 2. Derivamos respecto a $x$.

\begin{eqnarray*} \frac{d y}{d x} & = & (- p’ \sin (p) + p’) x + (\cos (p) + p) + \frac{1}{2} p’ \cos (p) \cos (p) – \frac{1}{2} p’ \sin (p) \sin (p) + \frac{1}{2} p’\\ \frac{d y}{d x} & = & (- p’ \sin (p) + p’) x + (\cos (p) + p) + \frac{1}{2} p’ \cos (p)^2 – \frac{1}{2} p’ \sin (p)^2 + \frac{1}{2} p’\\ \frac{d y}{d x} & = & – x p’ \sin (p) + x p’ + \cos (p) + p + \frac{1}{2} p’ \cos (p)^2 – \frac{1}{2} p’ \sin (p)^2 + \frac{1}{2} p’\\ \frac{d y}{d x} & = & (- x \sin (p) + x) p’ + \frac{1}{2} (\cos (p) ^2 – \sin (p)^2) p’ + \frac{1}{2} p’ + \cos (p) + p\\ \frac{d y}{d x} & = & \left[ (- x \sin (p) + x) + \frac{1}{2} (\cos (p) ^2 – \sin (p)^2) + \frac{1}{2} \right] p’ + \cos (p) + p \end{eqnarray*}

Paso 3. Despejamos para $x$.

Si $y’=p$, entonces:

\begin{eqnarray*} p & = & \left[ (- x \sin (p) + x) + \frac{1}{2} (\cos (p) ^2 – \sin (p)^2) + \frac{1}{2} \right] p’ + \cos (p) + p\\ 0 & = & \left[ (- x \sin (p) + x) + \frac{1}{2} (\cos (p) ^2 – \sin (p)^2) + \frac{1}{2} \right] p’ + \cos (p)\\ \left[ (- x \sin (p) + x) + \frac{1}{2} (\cos (p) ^2 – \sin (p)^2) + \frac{1}{2} \right] p’ & = & – \cos (p)\\ p’ & = & – \frac{\cos (p)}{(- x \sin (p) + x) + \frac{1}{2} (\cos (p) ^2 – \sin (p)^2) + \frac{1}{2}}\\ \frac{d p}{d x} & = & – \frac{\cos (p)}{(- x \sin (p) + x) + \frac{1}{2} (\cos (p) ^2 – \sin (p)^2) + \frac{1}{2}} \end{eqnarray*}

La ED anterior es lineal en $x$. de modo que:

\begin{eqnarray} \frac{d x}{d p} & = & – \frac{(- x \sin (p) + x) + \frac{1}{2} (\cos (p) ^2 – \sin (p)^2) + \frac{1}{2}}{\cos (p)} \nonumber\\ \frac{d x}{d p} & = & – \frac{1 – \sin (p)}{\cos (p)} x – \frac{1}{2} \frac{(\cos (p)^2 – \sin (p)^2)}{\cos (p)} – \frac{1}{2 \cos (p)} \nonumber\\ \frac{d x}{d p} + \frac{1 – \sin (p)}{\cos (p)} x & = & – \frac{1}{2} \frac{(\cos (p)^2 – \sin (p)^2)}{\cos (p)} – \frac{1}{2 \cos (p)} \nonumber\\ \frac{d x}{d p} + \frac{1 – \sin (p)}{\cos (p)} x & = & – \frac{1}{2} \left( \cos (p) – \frac{\sin (p)^2}{\cos (p)} + \frac{1}{\cos (p)} \right) …(5) \end{eqnarray}

Paso 4. Resolver la ED lineal.

Calculamos el factor integrante.

\begin{eqnarray*} {e^{\int P (p) d p}} & \Rightarrow & P (p) = \frac{1 – \sin (p)}{\cos (p)}\\ & \Rightarrow & P (p) = \frac{1 – \sin (p)}{\cos (p)} \frac{1 + \sin (p)}{1 + \sin (p)}\\ & \Rightarrow & P (p) = \frac{1 – \sin (p)^2}{\cos (p) (1 + \sin (p))}\\ & \Rightarrow & P (p) = \frac{\cos (p)^2}{\cos (p) (1 + \sin (p))}\\ & \Rightarrow & P (p) = \frac{\cos (p)}{1 + \sin (p)} \end{eqnarray*}

De modo que:

\begin{eqnarray*} e^{\int P (p) d p} & \Rightarrow & P (p) d p = \frac{\cos (p)}{1 + \sin (p)}\\ & \Rightarrow & \int P (p) d p = \int \frac{\cos (p)}{1 + \sin (p)} d p \end{eqnarray*}

Utilizando la fórmula: $\int u d u$, tenemos:

\begin{eqnarray*} u & = & 1 + \sin (p)\\ d u & = & \cos (p) \end{eqnarray*}

Por tanto:

\begin{eqnarray*} e^{\int P (p) d p} & \Rightarrow & \int P (p) d p = l n | 1 + \sin (p) | \end{eqnarray*}

De donde el factor integrante buscado, es:

$$e^{l n (1 + \sin (p))} = (1 + \sin (p))$$

De modo que multiplicando el factor integrante en la ED (5), tenemos:

\begin{eqnarray*} (1 + \sin (p)) \left( \frac{d x}{d p} + \frac{1 – \sin (p)}{\cos (p)} x \right) & = & (1 + \sin (p)) \left( – \frac{1}{2} \left( \cos (p) – \frac{\sin (p)^2}{\cos (p)} + \frac{1}{\cos (p)} \right) \right)\\ (1 + \sin (p)) \frac{d x}{d p} + (1 + \sin (p)) \frac{1 – \sin (p)}{\cos (p)} x & = & – \frac{1}{2} (1 + \sin (p)) \left( \cos (p) + \frac{1 – \sin (p)^2}{\cos (p)} \right)\\ \frac{d}{d p} ((1 + \sin (p)) x) & = & – \frac{1}{2} (1 + \sin (p)) \left( \cos (p) + \frac{\cos \left( p \right)^2 }{\cos (p)} \right)\\ d ((1 + \sin (p)) x) & = & \left( – \frac{1}{2} (1 + \sin (p)) (\cos (p) + \cos (p)) \right) d p\\ d ((1 + \sin (p)) x) & = & \left( – \frac{1}{2} (1 + \sin (p)) 2 \cos (p) \right) d p\\ d ((1 + \sin (p)) x) & = & – (\cos (p)) d p – (\cos (p) \sin (p)) d p \end{eqnarray*}

Integrando:

\begin{eqnarray*} \int d ((1 + \sin (p)) x) & = & – \int \cos (p) d p – \int \cos (p) \sin (p) d p\\ (1 + \sin (p)) x & = & – \sin (p) + \frac{1}{2} \cos (p)^2 + C \end{eqnarray*}

Por tanto:

\begin{eqnarray*} x & = & – \frac{\sin (p)}{1 + \sin (p)} + \frac{1}{2} \frac{\cos (p)^2}{(1 + \sin (p))} + \frac{C}{1 + \sin (p)}\\ x & = & \frac{\cos (p)^2 + 2 C – \sin (p)}{2 (1 + \sin (p))} \end{eqnarray*}

Paso 5. Soluciones paramétricas.

Sustituyendo en (4) el resultado anterior:

\begin{eqnarray*} y & = & (\cos (p) + p) x + \frac{1}{2} \sin (p) \cos (p) + \frac{1}{2} p\\ y & = & (\cos (p) + p) \left( \frac{\cos (p)^2 + 2 C – \sin (p)}{2 (1 + \sin (p))} \right) + \frac{1}{2} \sin (p) \cos (p) + \frac{1}{2} p \end{eqnarray*}

De modo que las ecuaciones paramétricas son:

\begin{eqnarray*} x & = & \frac{\cos (p)^2 + 2 C – \sin (p)}{2 (1 + \sin (p))}\\ y & = & (\cos (p) + p) \left( \frac{\cos (p)^2 + 2 C – \sin (p)}{2 (1 + \sin (p))} \right) + \frac{1}{2} \sin (p) \cos (p) + \frac{1}{2} p \end{eqnarray*}

Paso 6. Soluciones singulares

Corrobora que la ED no tiene soluciones singulares implementando la técnica anterior del Jacobiano.

---

Ejercicio 4.

Resolver:

$$y=\left( y’+3\right)-2\left( y’\right)^{2}$$

Solución.

Paso 1. Sustituimos $y’=p$.

$$y=\left( p+3\right)-2\left(p\right)^{2}…(6)$$

Paso 2. Derivar con respecto a $x$.

\begin{eqnarray*} \frac{d y}{d x} & = & x (p’) + (p + 3) – 4 p p’\\ \frac{d y}{d x} & = & (x – 4 p) p’ + p + 3 \end{eqnarray*}

Paso 3. Despejamos para $x$.

Si $y’=p$, entonces:

\begin{eqnarray*} p & = & (x – 4 p) p’ + p + 3\\ 0 & = & (x – 4 p) p’ + 3\\ (x – 4 p) p’ & = & – 3\\ p’ & = & – \frac{3}{x – 4 p}\\ \frac{d p}{d x} & = & \frac{- 3}{x – 4 p} \end{eqnarray*}

La ED anterior es lineal en $x$, de modo que:

\begin{eqnarray} \frac{d x}{d p} & = & – \frac{x – 4 p}{3} \nonumber\\ \frac{d x}{d p} & = & – \frac{x}{3} + \frac{4}{3} p \nonumber\\ \frac{d x}{d p} + \frac{x}{3} & = & \frac{4}{3} p …(7) \end{eqnarray}

Paso 4. Resolvemos la ED lineal.

Calculamos el facotr integrante.

\begin{eqnarray*} e^{\int P (p) d p} & \Rightarrow & P (p) = \frac{1}{3} \end{eqnarray*}

De modo que:

\begin{eqnarray*} e^{\int P (p) d p} & \Rightarrow & P (p) d p = \frac{1}{3} d p\\ & \Rightarrow & \int P (p) d p = \frac{1}{3} \int d p\\ & \Rightarrow & \int P (p) d p = \frac{1}{3} p \end{eqnarray*}

Por tanto, el factor integrante es:

$$e^{\int P (p) d p} = e^{\frac{1}{3} p}$$

Multiplicando el factor integrante por la ED (7), tenemos:

\begin{eqnarray*} e^{\frac{1}{3} p} \left( \frac{d x}{d p} + \frac{x}{3} \right) & = & e^{\frac{1}{3} p} \frac{4}{3} p\\ e^{\frac{1}{3} p} \frac{d x}{d p} + e^{\frac{1}{3} p} \frac{x}{3} & = & \frac{4}{3} p e^{\frac{1}{3} p}\\ \frac{d}{d p} \left( e^{\frac{1}{3} p} x \right) & = & \frac{4}{3} p e^{\frac{1}{3} p}\\ d \left( e^{\frac{1}{3} p} x \right) & = & \frac{4}{3} p e^{\frac{1}{3} p} d p \end{eqnarray*}

Integrando:

\begin{eqnarray*} \int d \left( e^{\frac{1}{3} p} x \right) & = & \frac{4}{3} \int p e^{\frac{1}{3} p} d p + C\\ e^{\frac{1}{3} p} x & = & \ldots \end{eqnarray*}

Para integrar el segundo miembro de la ecuación, utilizamos integración por partes:

$u=p$	$dv = e^{\frac{1}{3}p}dp$
$du=dp$	$v = 3\int{\frac{1}{3}e^{\frac{1}{3}p}}dp$
	$v = 3e^{\frac{1}{3}p}$

De modo que:

\begin{eqnarray*} e^{\frac{1}{3} p} x & = & \frac{4}{3} \int p e^{\frac{1}{3} p} d p + C\\ & = & \frac{4}{3} \left[ 3 p e^{\frac{1}{3} p} – 3 \int e^{\frac{1}{3} p} d p \right] + C\\ & = & \frac{4}{3} \left[ 3 p e^{\frac{1}{3} p} – 9 e^{\frac{1}{3} p} \right] + C\\ & = & 4 p e^{\frac{1}{3} p} – 12 e^{\frac{1}{3} p} + C \end{eqnarray*}

Por tanto:

$$x=4p-12+Ce^{-\frac{1}{3}p}$$

Paso 5. Soluciones paramétricas.

Sustituimos el resultado anterior en la ED (6), de modo que:

\begin{eqnarray*} y & = & x (p + 3) – 2 p^2\\ y & = & \left( 4 p – 12 + C e^{- \frac{1}{3} p} \right) (p + 3) – 2 p^2 \end{eqnarray*}

De modo que las ecuaciones paramétricas son:

\begin{eqnarray*} x & = & 4 p – 12 + C e^{- \frac{1}{3} p}\\ y & = & \left( 4 p – 12 + C e^{- \frac{1}{3} p} \right) (p + 3) – 2 p^2 \end{eqnarray*}

Paso 6. Soluciones singulares.

Utilizamos el determinante de la matriz jacobiana igualada a $0$, para despejar $C=C(p)$ y sustituir los resultados en las euaciones parametricas para obtner la envolvente (o solución singular).

\begin{eqnarray*} \det \left( \begin{array}{cc} X_c & Y_c\\ X_p & Y_p \end{array} \right) & = & 0\\ \det \left( \begin{array}{cc} e^{- \frac{1}{3} p} & (p + 3) e^{- \frac{1}{3} p}\\ – \frac{1}{3} C e^{- \frac{1}{3} p} + 4 & – \frac{1}{3} \left( C e^{- \frac{1}{3} p} – 12 \right) (p + 3) + C e^{- \frac{1}{3} p} – 12 \end{array} \right) & = & 0 \end{eqnarray*}

Desarrollando, obtenemos:

$$C = 12 e^{\frac{1}{3} p}$$

Sustituyendo éste resultado en las ecuaciones paramétricas, estas se convierten en:

\begin{eqnarray*} x & = & 4 p\\ y & = & 4 p (p + 3) – 2 p^2 \end{eqnarray*}

Con el cual podemos graficar o también podemos sustituir el valor de p la ecuación (6), de donde:

\begin{eqnarray*} y & = & x \left( \frac{x}{4} + 3 \right) – 2 {\left( \frac{x}{4} \right)^2} \\ y & = & \frac{x^2}{4} + 3 x – \frac{2 x^2}{16}\\ y & = & \frac{1}{8} x^2 + 3 \end{eqnarray*}

Siendo la envolvente o solución singular:

$$y = \frac{1}{8} x^2 + 3$$

Gráfica de la envolvente.

La gráfica de la envolvente junto con las rectas solución es:

---

Ejercicio 5.

Resolver:

$$y = x (y’)^2 – y’$$

Solución.

Paso 1. Sustituimos $y’=p$.

$$y=xp^{2}-p … (8)$$

Paso 2. Derivar respecto a $x$.

\begin{eqnarray*} \frac{d y}{d x} & = & 2 x p p’ + p^2 – p’\\ \frac{d y}{d x} & = & (2 x p – 1) p’ + p^2 \end{eqnarray*}

Paso 3. Despejamos para $x$.

Si $y’=p$, entonces:

\begin{eqnarray*} \frac{d y}{d x} & = & (2 x p – 1) p’ + p^2\\ p & = & (2 x p – 1) p’ + p^2\\ (2 x p – 1) p’ & = & p – p^2\\ p’ & = & \frac{p – p^2}{2 x p – 1}\\ \frac{d p}{d x} & = & \frac{p (1 – p)}{2 x p – 1} \end{eqnarray*}

Ésta ecuación es lineal en $x$, de tal modo que:

\begin{eqnarray} \frac{d x}{d p} & = & \frac{2 x p – 1}{p (1 – p)} \nonumber\\ \frac{d x}{d p} & = & \frac{2}{1 – p} x – \frac{1}{p (1 – p)} \nonumber\\ \frac{d x}{d p} – \frac{2}{1 – p} x & = & – \frac{1}{p (1 – p)} … (9) \end{eqnarray}

Paso 4. Resolvemos la ED lineal.

Calculamos el factor integrante:

\begin{eqnarray*} e^{\int P (p) d p} & \Rightarrow & P (p) = – \frac{2}{1 – p}\\ & \Rightarrow & P (p) d p = – \frac{2}{1 – p} d p\\ & \Rightarrow & \int P (p) d p = – \int \frac{2}{1 – p} d p\\ & \Rightarrow & \int P (p) d p = – 2 \int \frac{- d p}{1 – p}\\ & \Rightarrow & \int P (p) d p = 2 l n (1 – p) \end{eqnarray*}

De modo que el factor integrante es:

$$e^{l n (1 – p)^{- 2}} = (1 – p)^2$$

Multiplicando el factor integrante por la ED (9):

\begin{eqnarray*} (1 – p)^2 \left( \frac{d x}{d p} – \frac{2}{1 – p} x \right) & = & – (1 – p)^2 \frac{1}{p (1 – p)}\\ (1 – p)^2 \frac{d x}{d p} – (1 – p)^2 \frac{2}{1 – p} x & = & – \frac{1 – p}{p}\\ (1 – p)^2 \frac{d x}{d p} – 2 (1 – p) x & = & – \frac{1 – p}{p}\\ \frac{d}{d p} ((1 – p)^2 x) & = & – \frac{1 – p}{p}\\ d ((1 – p)^2 x) & = & – \frac{1 – p}{p} d p \end{eqnarray*}

Integrando:

\begin{eqnarray*} \int d ((1 – p)^2 x) & = & – \int \frac{d p}{p} + \int d p + C\\ (1 – p)^2 x & = & – l n (p) + p + C\\ x & = & – \frac{l n (p) + p + C}{(1 – p)^2} \end{eqnarray*}

Paso 5. Soluciones paramétricas.

Sustituyendo el resultado anterior en la ED (8), tenemos:

\begin{eqnarray*} y & = & x p^2 – p\\ y & = & – \frac{l n (p) + p + C}{(1 – p)^2} p^2 – p \end{eqnarray*}

De modo que las ecuaciones paramétricas, son:

\begin{eqnarray*} x & = & – \frac{l n (p) + p + C}{(1 – p)^2}\\ y & = & – \frac{l n (p) + p + C}{(1 – p)^2} p^2 – p \end{eqnarray*}

Paso 6. Soluciones singulares

Buscamos eliminar el parámetro $p$,como siempre,para poder encontrar la solución singular.

Podemos notar de las ecuaciones paramétricas que $p=0$, lo cual daría la solución singular $y=0$,que ciertamente es una solución de la ED.

Si derivamos la ED (8) respecto de $p$ e igualando a cero la derivada, para poder encontrar la tangente a $y$, vemos que el resultado no depende de x, de modo que podemos despejarla:

\begin{eqnarray*} y & = & x p^2 – p\\ \frac{d y}{d x} & = & 2 x p – 1\\ 0 & = & 2 x p – 1\\ 2 x p & = & 1\\ x & = & \frac{1}{2 p} \end{eqnarray*}

Despejando $p$ para poder sustituir en $y$ nuevamente:

$$p = \frac{1}{2 x}$$

Esto implica:

\begin{eqnarray*} y & = & x \left( \frac{1}{2 x} \right)^2 – \frac{1}{2 x}\\ y & = & \frac{1}{4 x} – \frac{1}{2 x} = \frac{1 – 2}{4 x}\\ y & = & – \frac{1}{4 x} \end{eqnarray*}

La soluciones $y=-1/(4x)$ y $y=0$, son soluciones singulares de la ED (8), donde la $y=0$, demarca el lugar geométrico de los puntos de retroceso de la famila de curvas solucion y $y=-1/(4x)$, delimita, a manera de envolvente, a las curvas solución de la ED de lagrange. Ver la siguiente figura.

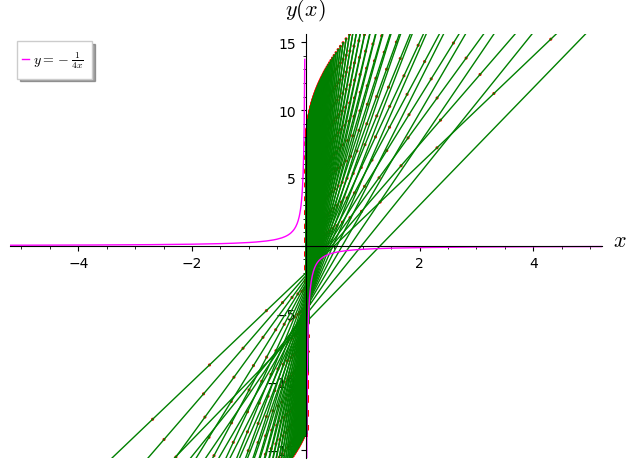
Si quieres automatizar tus soluciones con programación, utilizando un programa potente y fácil de aprender como sagemath, te recomendamos nuestra: Calculadora de ecuaciones diferenciales lagrange (codigo), para que estes seguro de tus soluciones, no pierdas tiempo y puedas hacer simulación.

Conviertete en un Expert@.

Te invitamos a profundizar en el tema y convertirte en un experto en ecuaciones diferenciales de Lagrange.

Para ello, te recomendamos adquirir nuestro producto: Calculadora de ecuaciones diferenciales lagrange (código), donde encontrarás 6 ejemplos resueltos paso a paso con sagemath de los ejercicios que están en ésta publicación y un ejemplo adicional de regalo, con la misma secuencia de solución que encuantras en ésta publicación para que te sea muy fácil seguir los pasos aún y cuando estés empezando a programar con sagemath.

Más aún, automatiza todas tus ecuaciones diferenciales de primer orden con nuestro producto: Sagemath y Python – Ecuaciones Diferenciales 1er Orden Lineales y No-Lineales (código).

Lleva tu conocimiento al siguiente nivel

Además, si deseas llevar tu comprensión y habilidades al siguiente nivel, te ofrecemos cursos especializados en ecuaciones diferenciales e inteligencia artificial, diseñados para estudiantes y profesionales que deseen dominar este campo de estudio haciendo uso de las herramientas de última generación.

Equipate con el conocimiento y las herramientas necesarias para abordar con confianza y éxito problemas de ecuaciones diferenciales de Lagrange, series de potencias para resolver ecuaciones diferenciales (EDs), sistemas de EDs lineales y no-lineales y más aún sistemas de EDs con inteligencia artificial, así como para aplicar este conocimiento en diversos campos de estudio y aplicaciones prácticas.

¡Haz clic en los enlaces a continuación para obtener más información y comenzar tu posisionamiento en el pináculo de tu sector iniciando un viaje hacia la maestría en ecuaciones diferenciales con inteligencia artificial!

Cursos especializados.

• ¿Qué son las Ecuaciones Diferenciales?
• Ecuaciones Diferenciales de primer orden lineales y no lineales
• Ecuaciones Diferenciales con Series de Potencias
• Caos y Ecuaciones Diferenciales

En nuestro curso, aprenderás a modelar matemáticamente poblaciones y a simularlas mediante métodos numéricos.

• Ecuaciones Diferenciales, Modelado, Aplicaciones e Inteligencia Artificial

El deseo de dominar las ecuaciones diferenciales de manera integral se hará evidente a medida que descubras el valor añadido que ofrecemos. Desde el modelado matemático hasta la programación simbólica y numérica, nuestro programa te sumerge en una experiencia educativa única, despierta tu curiosidad y te impulsa a alcanzar nuevos niveles de conocimiento y habilidad.

Conviértete en un experto en ecuaciones diferenciales de Lagrange y lleva tus habilidades matemáticas al siguiente nivel. ¡El conocimiento está a tu alcance!

¿Encontraste lo que buscabas?

¿Quieres comenzar desde cero? te recomiendo nuestro artículo: Tipos de ecuaciones diferenciales ordinarias de primer orden y su clasificación.

¿Quiero una visión general desde cero? te recomiendo nuestro artículo: Domina las Ecuaciones Diferenciales Ordinarias: Guía Esencial 2024.

¿Quieres más profuncdidad en el conocimiento de las ecuaciones no-lineales de pimer orden? te recomiendo nuestros artículos:

• Ecuaciones Diferenciales de Riccati
• Ecuaciones Diferenciales de Clairaut
• Ecuaciones Diferenciales de Bernoulli
• Tipos de ecuaciones diferenciales ordinarias de primer orden
• Domina las Ecuaciones Diferenciales Ordinarias: Guía Esencial 2024