Introducción
En el fascinante campo de las ecuaciones diferenciales, nos enfrentamos a desafíos intrigantes que no solo ponen a prueba nuestras habilidades matemáticas, sino que también nos permiten explorar conceptos fundamentales. En este artículo, exploraremos en detalle el Problema 15 del libro de Dennis G. Zill, 7ª Edición, y ofreceremos una solución paso a paso. Más allá de la resolución, profundizaremos en el Método del Factor Integrante, una herramienta valiosa para abordar ecuaciones diferenciales lineales de primer orden. Si eres estudiante de ingeniería, ciencias exactas o un profesional comprometido con tu mejora continua, este artículo te proporcionará una visión enriquecedora.
El Poder del Método: Factor Integrante
Antes de sumergirnos en la resolución del problema, es importante destacar el Método del Factor Integrante, que nos brinda una forma sistemática de abordar ecuaciones diferenciales lineales de primer orden en cuatro pasos sencillos.
Metodología
Antes de abordar el problema, es importante comprender la metodología que utilizaremos. La resolución de ecuaciones diferenciales lineales de primer orden implica cuatro pasos fundamentales:
Paso 1: Forma Estándar: Comenzamos por expresar la ecuación en su forma estándar: $\frac{dy}{dx}+P(x)y=f(x)$.
Paso 2: Factor Integrante: Calculamos el Factor Integrante, que es esencial para simplificar la ecuación. En nuestro caso, el Factor Integrante es $e^{\int P(x)dx}$.
Forma de solución: $y={{y}_{c}}+{{y}_{p}}$
Paso 3: Solución del Sistema Homogéneo Asociado: Resolvemos el sistema homogéneo asociado, que se obtiene eliminando el término no homogéneo. La solución general se expresa como: ${{y}_{c}}=C{{e}^{-\mathop{\int }^{}P\left( x \right)dx}}$
Paso 4: Solución Particular del Sistema No Homogéneo: Finalmente, encontramos una solución particular para el sistema no homogéneo utilizando la fórmula
$x_p=\frac{1}{e^{\int P(x)dx}}\int e^{\int P(x)dx}f(x)dx$.
Ejercicios 2.3 Libro Dennis G. Zill (Problema 15)
a) $\Large ydx-4\left( x+{{y}^{6}} \right)dy=0$
Desarrollo:
Ahora, apliquemos esta metodología al Problema 15 del libro de Dennis G. Zill:
Problema 15: Dada la ecuación diferencial $ydx-4(x+y^6)dy=0$, nuestra tarea es resolverla paso a paso.
I. El primer paso consiste en escribir la forma estándar de la ED a resolver:
En este caso identificamos que la variable independiente es la que usualmente es la variable dependiente, es decir, “y” es la variable independiente y “x” es la dependiente. Esto lo podemos fácilmente notar en una ED lineal de 1er orden (expresada explícitamente), si nos percatamos de que el coeficiente que se encuentra al frente de la derivada de “dx” depende solo de una variable y esta es contraria a “x”.
Dividimos, entonces, entre el coeficiente de , que es “y”[ecuación a)], los coeficientes de los demás términos de la ecuación que dependen de “y”.
Por último agrupamos términos semejantes y simplificamos.
$\frac{dx}{dy}+P\left( y \right)x=f(y)$
$\frac{dx}{dy}-\frac{4(x+{{y}^{6}})}{y}=0$,
$\frac{dx}{dy}-\frac{4x}{y}-\frac{4{{y}^{6}}}{y}=0$
$\frac{dx}{dy}-\frac{4x}{y}=4{{y}^{5}}$
II. En el segundo paso encontramos el factor integrante:
Para esto sustituimos el valor de P(y) en ${{e}^{\mathop{\int }^{}P\left( y \right)dy}}$, donde: P(y)=$-\frac{4}{y}$. Para recordar las formulas integrales y el manejo de las funciones trascendentes vea el final del ejercicio.
${{\mathbf{e}}^{\mathop{\int }^{}\mathbf{P}\left( \mathbf{y} \right)\mathbf{dy}}}$,
${{e}^{-4\mathop{\int }^{}\frac{dy}{y}}}={{e}^{-4\ln y}}$
$={{e}^{\ln {{y}^{-4}}}}$
$={{y}^{-4}}$
III. Como tercer paso, encontramos la familia de soluciones del sistema homogéneo asociado:
Recordemos que el sistema homogéneo asociado, en este caso, es la ecuación diferencial: $\frac{dx}{dy}-\frac{4x}{y}=0$ . Para resolverla sustituimos en la fórmula: ${{x}_{c}}=C{{e}^{-\mathop{\int }^{}P\left( y \right)dy}}$, los valores de P(y)=$~-\frac{4}{y}$, encontrado en el primer paso, con anterioridad, y desarrollamos. Para esclarecer de donde sale la fórmula ${{x}_{c}}=C{{e}^{-\mathop{\int }^{}P\left( y \right)dy}}$, siga el siguiente enlace: Solución del sistema homogéneo asociado.
${{x}_{c}}=C{{e}^{\left( – \right)-4\mathop{\int }^{}\frac{dy}{y}}}$
$=C{{e}^{4\ln y}}$
$=C{{e}^{\ln {{y}^{4}}}}$
$=C{{y}^{4}}$
Se puede ver una solución particular $x=-3{{y}^{4}}$, donde $C=-3$
Notar que la función ${{x}_{c}}=C{{y}^{4}}$ , tiene como dominio todo el conjunto de los números reales. El intervalo de definición de una solución, por definición (ver Intervalo de definición de una solución I), necesita cumplir al menos 2 criterios para ser considerado válido: 1. Que la función solución que se encuentra esté definida en él (no necesariamente continua, una función definida por partes también puede calificar), y 2. Que esta función sea, también, derivable dentro del intervalo.
IV. En el cuarto paso, encontramos una solución particular a partir del sistema no homogéneo:
El sistema no homogéneo, en este caso, es la ecuación diferencial: $\frac{dx}{dy}-\frac{4x}{y}=4{{y}^{5}}$, que representa la familia de soluciones particulares de la ED lineal. Para resolverla utilizamos la fórmula: ${{x}_{p}}=\frac{1}{{{e}^{\mathop{\int }^{}P\left( y \right)dy}}}\mathop{\int }^{}{{e}^{\mathop{\int }^{}P\left( y \right)dy}}f(y)dy$ , donde: ${{e}^{\mathop{\int }^{}P\left( y \right)dy}}={{y}^{-4}}$ (obtenido en el punto ii.) y $f\left( y \right)=4{{y}^{5}}$, obtenido en el punto i. Notar que la fórmula:
${{x}_{p}}=\frac{1}{{{e}^{\mathop{\int }^{}P\left( y \right)dy}}}\mathop{\int }^{}{{e}^{\mathop{\int }^{}P\left( y \right)dy}}f(y)dy$, es solo la contraparte de la fórmula: ${{y}_{p}}=\frac{1}{{{e}^{\mathop{\int }^{}P\left( x \right)dx}}}\mathop{\int }^{}{{e}^{\mathop{\int }^{}P\left( x \right)dx}}f(x)dx$ , para ver de dónde salen estas siga el enlace siguiente:
solución del sistema no homogeneo.
${{x}_{p}}=\frac{1}{{{y}^{-4}}}\mathop{\int }^{}{{y}^{-4}}(4{{y}^{5}})dx$
$=\frac{4}{{{y}^{-4}}}\mathop{\int }^{}\text{y}dx$
$=\frac{4}{{{y}^{-4}}}(\frac{1}{2}{{y}^{2}})$
$=2{{y}^{6}}$
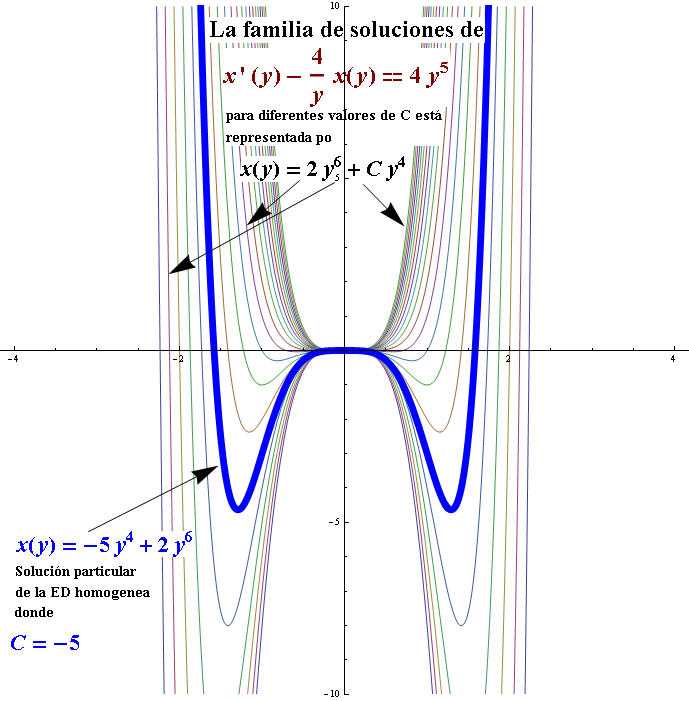
Se puede ver una solución particular $x\left( y \right)=-5{{y}^{4}}+2{{\text{y}}^{6}}$,
Donde: $C=-5$. Nuevamente notar que la función $x=C{{y}^{4}}+2{{y}^{6}}$ , tiene como dominio todo el conjunto de los números reales. Por definición (ver Intervalo de definición de una solución I), el intervalo que contiene la solución de una ED, debe cumplir con 2 criterios: que la función esté definida y sea derivable en dicho intervalo.
Por tanto, la solución general de la ecuación diferencial $ydx-4\left( x+{{y}^{6}} \right)dy=0$, es: $\Large x=C{{y}^{4}}+2{{y}^{6}}$
Notar que:
$a\ln x=\ln {{x}^{a}}$
Debido a que:
$y={{e}^{x}}$implica $x=\ln y$ y además $\ln y={{\log }_{e}}y$ recordamos que la función $x={{\log }_{e}}y$, es inversa de $y={{e}^{x}}$, por tanto si multiplicamos esta última función por lnobtendremos:
$\ln y=\ln {{e}^{x}}=x$ y
${{e}^{x}}={{e}^{\ln y}}=y$
Programa Completo Ecuaciones Diferenciales
- Realizar Modelado Matemático
- Aplicar los algoritmos de solución. Te enseñamos a saber:
- ¿Por donde Empezar cuando tengo una ED enfrente?
- ¿Qué tipo de Ecuacion Diferencial tengo enfrente?
- ¿Qué método emplear para resolve la ED que tengo enfrente?
- Realizar simulación por computadora (simbólica y numérica) para transformar tu realidad y la de tu entorno, brindando servicio efectivo y sintiendote realizado como ingeniero, como matemñatico aplicado
- Inscríbete a nuestro PROGRAMA COMPLETO de ECUACIONES DIFERENCIALES


