
| Sección | Resumen |
|---|---|
| 1. Motivación para estudiar | Destacamos la importancia de abordar las Ecuaciones Diferenciales No-Lineales de Riccati, prometiendo una respuesta efectiva. |
| 2. Reflejos de la humanidad | ¿Quién fue Jacopo Francesco Riccati? Se habla sobre el tema de dónde surge su célebre ecuación aquí estudiada y datos de trascendentes de su vida. |
| 3. Aplicaciones de la ED de Riccati | Ejemplos de áreas donde se puede encontar la ecuación diferencial de Riccati, modelando fenómenos |
| 4. Metodología | Definición de pasos claros para abordar Ecuaciones Diferenciales No-Lineales de Riccati. |
| 5. Ejercicios Resueltos | Resolución paso a paso de ejercicios específicos utilizando la metodología presentada. |
| 6. Conviértete en un EXPERT@ | Desbloquea tu potencial y alcanza la maestría en Ecuaciones Diferenciales e Inteligencia Artificial |
Motivación para estudiar
Si lees hasta el final éste artículo, Ecuaciones Diferenciales No-Lineales: Riccati, superarás la frustración asociada con la percepción de dificultad que rodea a estas ecuaciones. Las ecuaciones de Riccati a menudo intimidan a estudiantes y docentes, pero este artículo está diseñado para cambiar esa perspectiva.
Nos sumergiremos en el corazón de estas ecuaciones, proporcionándote una comprensión profunda y mostrándote cómo aplicar de manera efectiva los algoritmos de solución para la Ecuación Diferencial de Riccati.
Al finalizar este artículo, no solo habrás conquistado la dificultad percibida de las ecuaciones de Riccati, sino que también encontrarás respuestas prácticas y tangibles que despejarán cualquier preocupación sobre su aplicabilidad en diversos contextos. Además, te brindaremos la oportunidad de profundizar aún más con el artículo de venta: Ecuaciones Diferenciales de Primer Orden Sagemath Python Lineales y No Lineales paso a paso.
Transforma tus percepciones y conviertete en un experto en la resolución de Ecuaciones Diferenciales No-Lineales de Riccati.
No hay problema que pueda aguantar el ataque sostenido del pensamiento
~Voltaire
Reflejos de la humanidad y datos importantes
Jacopo Francesco Riccati (1676-1754), matemático italiano, contribuyó significativamente a la difusión de las teorías de Newton y realizó investigaciones en hidrodinámica. Su trabajo en ecuaciones diferenciales lo llevó a descubrir una solución particular para un tipo específico de ecuación, conocida como la ecuación de Riccati. Esta ecuación, inventada y desarrollada en el siglo XVIII, tenía como objetivo analizar problemas hidrodinámicos.
La motivación detrás del desarrollo de la técnica para resolver la ecuación de Riccati se encuentra en su interés por comprender los fenómenos de flujo de fluidos y la dinámica de fluidos. Riccati se enfrentó a desafíos en la modelización matemática de estos problemas, y la ecuación de Riccati se convirtió en una herramienta fundamental en su búsqueda de soluciones.

En cuanto a su vida personal, Riccati experimentó pérdidas significativas. Su padre falleció cuando él era joven, lo que pudo haber influido en su dedicación a las matemáticas y su búsqueda de respuestas en el mundo científico. Además, se le ofreció la presidencia de la Academia de Ciencias de San Petersburgo, una posición prestigiosa, pero la rechazó. La razón detrás de esta decisión no fue por falta de reconocimiento o ambición, sino más bien por su afán de continuar su trabajo científico y matemático. Optó por seguir su pasión y contribuir al avance del conocimiento en lugar de asumir una posición administrativa.
Jacopo Francesco Riccati dejó un legado importante en las matemáticas y la hidrodinámica, y su ecuación sigue siendo relevante en la resolución de problemas no lineales de primer orden. Su enfoque en la investigación y su rechazo de la presidencia de la Academia de ciencias de San Petesburgo, que una vez le ofrecieron y rechazó por permiirse una vida retirada y dedicada al estudio, demuestran su compromiso con la ciencia y su deseo de contribuir al conocimiento en lugar de buscar reconocimiento personal.
Aplicaciones de la ecuación diferencial de Riccati
La Ecuación Diferencial (ED) de Riccati tiene diversas aplicaciones en diversos campos, entre las cuales destacan:

1. Mecánica clásica: La ecuación de Riccati aparece en el estudio del movimiento de una partícula en un potencial central, como el potencial gravitatorio o el potencial electrostático. Permite determinar la trayectoria de la partícula en función de su energía y momento angular.
2. Óptica: La ecuación de Riccati se utiliza para modelar la propagación de la luz en guías de onda ópticas. Permite calcular el campo electromagnético dentro de la guía de onda y determinar las condiciones para la transmisión de la luz.
3. Control de sistemas: La ecuación de Riccati se utiliza en el diseño de controladores para sistemas dinámicos. Permite encontrar un controlador que optimice el comportamiento del sistema, como minimizar el error de seguimiento o mejorar la estabilidad de sistemas lineales y no lineales.

4. Optimización financiera: La ecuación de Riccati también se utiliza en la optimización financiera, especialmente en la modelización de carteras de inversión y en la gestión de riesgos. Ayuda a encontrar estrategias óptimas para maximizar el rendimiento o minimizar el riesgo en entornos financieros.
Otras aplicaciones
- Teoría de la filtración: La ecuación de Riccati se utiliza para modelar el proceso de filtración de señales.
- Procesamiento de imágenes: La ecuación de Riccati se utiliza en el procesamiento de imágenes para eliminar el ruido y mejorar la calidad de la imagen.
- Econometría: La ecuación de Riccati se utiliza en econometría para modelar el comportamiento de los mercados financieros.
- Mecánica Cuántica: En el contexto de la mecánica cuántica, la ED de Riccati surge al modelar la función de onda de partículas subatómicas en ciertos potenciales cuadráticos. Su solución proporciona información valiosa sobre los estados cuánticos.
Metodología
La metodología propuesta para abordar la Ecuación Diferencial (ED) de Riccati se presenta en tres pasos estructurados y eficaces:
- Formulación de la Ecuación Diferencial de Riccati:
- Escribimos la forma estándar de la ED: $$\frac{dy}{dx} = a(x)y^2 + b(x)y + c(x)$$ y definimos si es una ED de Riccati.
- Transformación a una Ecuación de Bernoulli:
- En caso de conocer una solución particular $$y_1=f(x)$$, transformamos la ED a una ED de Bernuolli mediante dos sustituciones consecutivas
- Reducción a una Ecuación Diferencial Lineal mediante Sustituciones:
- Se realiza la primera sustitución: $$y = y_1 + u$$, donde $u = f(x)$. Esto permite obtener una ED de Bernoulli con $n=2$, según la técnica descrita en nuestro artículo Ecuaciones Diferenciales de Bernoulli
- Posteriormente, se lleva a cabo la segunda sustitución: $$w = u^{-1}$$, reduciendo finalmente la ecuación a una forma lineal más manejable. Para ecuaciones de Bernoulli donde $n≠2$, consulta nuestro artículo: Ecuaciones Diferenciales de Bernoulli.
Con ésta metodología proporciona un enfoque estructurado y claro para la resolución de la ED de Riccati.
Ecuaciones Diferenciales No-lineales Ejercicios Resueltos: Riccati, paso a paso
Ejercicio 1.
Resolver:
$$\frac{dy}{dx}-\left(1-x\right)y^{2}=\left(2x-1\right)y-x$$
Suponer una solución $y_1=1$
Solución.
Paso 1. Forma estándar:
$$ \begin{eqnarray*} \frac{d y}{d x} – (1 – x) y^2 & = & (2 x – 1) y – x\\ y’ & = & (1 – x) y^2 + (2 x – 1) y – x \end{eqnarray*} $$Paso 2.
Sí, es una ED de Riccati, por tanto transformamos a una ED de Bernoulli. Tenemos que $y_1=1$, es una solución conocida de la ED, por tanto.
Paso 3.
Primera Sustitución con $y=1+u$, de modo que, $\frac{dy}{dx}=\frac{du}{dx}$, de modo que:
$$ \begin{eqnarray*} y’ & = & (1 – x) y^2 + (2 x – 1) y – x\\ \frac{d u}{d x} & = & (1 – x) (1 + u)^2 + (2 x – 1) (1 + u) – x\\ \frac{d u}{d x} & = & (1 – x) (1 + 2 u + u^2) + 2 x + 2 u x – 1 – u – x\\ \frac{d u}{d x} & = & 1 + 2 u + u^2 – x – 2 u x – x u^2 + 2 x + 2 u x – 1 – u – x\\ \frac{d u}{d x} & = & 1 + 2 u + u^2 – x – x u^2 + 2 x – 1 – u – x\\ \frac{d u}{d x} & = & 2 u + u^2 – x – x u^2 + 2 x – u – x\\ \frac{d u}{d x} & = & 2 u + u^2 – x u^2 – u\\ \frac{d u}{d x} & = & (1 – x) u^2 + u \end{eqnarray*} $$De modo que obtenemos la ED de Bernoulli:
$$\frac{du}{dx}-u=(1-x)u^{2}$$
Segunda sustitución: $u=w^{-1}$ para resolver la ED de Bernoulli, donde, $\frac{du}{dx} = -w^{-2}\frac{dw}{dx}$. De modo que:
$$ \begin{eqnarray*} \frac{d u}{d x} – u & = & (1 – x) \frac{1}{w^2}\\ – \frac{1}{w^2} \frac{d w}{d x} – \frac{1}{w} & = & (1 – x) \frac{1}{w^2}\\ – \frac{d w}{d x} – w & = & 1 – x\\ \frac{d w}{d x} + w & = & x – 1 \end{eqnarray*} $$La ED anterior es una lineal de primer orden. Para resolverla, utilizaremos el algoritmo desarrollado en nuestro artículo: Factores Integrantes. Por tanto, procedemos de la siguiente forma. Calculamos el factor integrante para la ED anterior:
$$e^{\int{P(x)dx}}$$
Para nuestro caso: $P(x)=1$, de modo que:
$$ \begin{eqnarray*} \int P (x) d x & = & \int d x\\ \int P (x) d x & = & x \end{eqnarray*} $$Es decir, el factor integrante buscado es:
$$e^{\int{P(x)dx}}=e^{x}$$
Esto implica:
$$ \begin{eqnarray*} e^x \left( \frac{d w}{d x} + w \right) & = & e^x (x – 1)\\ e^x \frac{d w}{d x} + e^x w & = & x e^x – e^x\\ \frac{d}{d x} (e^x w) & = & x e^x – e^x\\ d (e^x w) & = & (x e^x – e^x) d x\\ \int d (e^x w) & = & \int x e^x d x – \int e^x d x + C \end{eqnarray*} $$Ahora, integrando por partes la integral $\int{x e^{x}}d x$,(ver el artículo: Factores Integrantes), procedemos de la siguiente forma.
Integramos por partes:
| $u=x$ | $dv=e^{x}dx$ |
| $du=dx$ | $v=e^{x}$ |
De modo que:
$$ \begin{eqnarray*} \int d (e^x w) & = & \int x e^x d x – \int e^x d x + C\\ \int d (e^x w) & = & \left[ x e^x – \int e^x d x \right] – \int e^x d x + C\\ e^x w & = & x e^x – 2 \int e^x d x + C\\ e^x w & = & x e^x – 2 e^x + C\\ w & = & x – 2 + C e^{- x} \end{eqnarray*} $$Regresando a las variables originales:
$$ \begin{eqnarray*} \frac{1}{u} & = & x – 2 + Ce^{- x}\\ \frac{1}{x – 2 + C e^{- x}} & = & u\\ y – 1 & = & \frac{1}{x – 2 + C e^{- x}}\\ y & = & \frac{1}{x – 2 + C e^{- x}} + 1 \end{eqnarray*} $$Por tanto la solución de la ED de Riccati (y Bernoulli), es:
$$y=\frac{1}{x-2+Ce^{-x}}+1$$
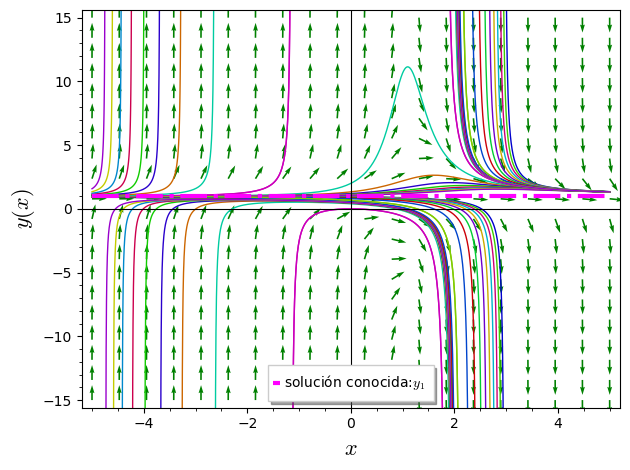
Si quieres aprender a automatizar tus resultados y tener la seguridad de los pasos que estás obteniendo te dejo nuestro recurso: Ecuaciones Diferenciales de Primer Orden Sagemath Python Lineales y No Lineales paso a paso.
Ejercicio 2.
Resolver:
$$y’=\frac{y}{x}+x^{2}y^{2}-x^{4}$$
Suponemos una solución: $y_1=x$.
Solución.
Paso 1. Forma estándar:
$$y’=x^{2}y^{2}+\frac{1}{x}y-x^{4}$$
Paso 2. Sí, es una ED de Riccati, por tanto transformamos a una ED de Bernoulli.
Tenemos que &y_1=x&, es una solución conocida de la ED, por tanto:
Paso 3. Primera sustición con $y=x+u$, de modo que, $\frac{dy}{dx}=1+\frac{du}{dx}$, de modo que:
$$ \begin{eqnarray*} y’ & = & x^2 y^2 + \frac{1}{x} y – x^4\\ 1 + \frac{d u}{d x} & = & x^2 {(x + u)^2} + \frac{1}{x} (x + u) – x^4\\ \frac{d u}{d x} & = & x^2 (x^2 + 2 x u + u^2) + 1 + \frac{u}{x} – x^4 – 1\\ \frac{d u}{d x} & = & x^4 + 2 x^3 u + x^2 u^2 + 1 + \frac{u}{x} – x^4 – 1\\ \frac{d u}{d x} & = & x^2 u^2 + \left( 2 x^3 + \frac{1}{x} \right) u\\ \frac{d u}{d x} – \left( 2 x^3 + \frac{1}{x} \right) u & = & x^2 u^2 \end{eqnarray*} $$De modo que obtenermos la ED de Bernoulli:
$$\frac{du}{dx}-\left(2x^{3}+\frac{1}{x}\right)u=x^{2}u^{2}$$
Donde $n=2$, según el algoritmo del artículo: Ecuaciones Diferenciales de Bernoulli.
Segunda sustitución: $u=w^{-1}$ para resolver la ED de Bernoulli, donde, $\frac{du}{dx}=-w^{-2}\frac{dw}{dx}$, de modo que:
$$ \begin{eqnarray*} \frac{d u}{d x} – \left( 2 x^3 + \frac{1}{x} \right) u & = & x^2 u^2\\ – \frac{1}{w^2} \frac{d w}{d x} – \left( 2 x^3 + \frac{1}{x} \right) \left( \frac{1}{w} \right) & = & x^2 \left( \frac{1}{w} \right)^2\\ \frac{1}{w^2} \frac{d w}{d x} + \left( 2 x^3 + \frac{1}{x} \right) \left( \frac{1}{w} \right) & = & – x^2 \frac{1}{w^2}\\ \frac{d w}{d x} + \left( 2 x^3 + \frac{1}{x} \right) w & = & – x^2 \end{eqnarray*} $$De este modo, como sabemos, obtenemos una ED lineal de primer orden y para reslverla, utilizaremos el algoritmo desarrollado en nuestro artículos: Factores integrantes. Por tanto, obtenemos el factor integrante:
$$e^{\int{P(x)}dx}$$
Para nuestro caso: $P(x)=2x^{3}+\frac{1}{x}$, de modo que:
$$ \begin{eqnarray*} \int P (x) d x & = & \int d x\\ \int P (x) d x & = & 2 \int x^3 d x + \int \frac{1}{x} d x\\ \int P (x) d x & = & \frac{2}{4} x^4 + l n (x) \end{eqnarray*} $$Es decir, el factor integrante buscado es:
$$ \begin{eqnarray*} e^{\int P (x) d x} & = & e^{\left( \frac{x^4}{2} + l n (x) \right)}\\ e^{\int P (x) d x} & = & x e^{\frac{x^4}{2}} \end{eqnarray*} $$Esto implica:
$$ \begin{eqnarray*} x e^{\frac{x^4}{2}} \left[ \frac{d w}{d x} + \left( 2 x^3 + \frac{1}{x} \right) w \right] & = & – x^3 e^{\frac{x^4}{2}}\\ x e^{\frac{x^4}{2}} \frac{d w}{d x} + x e^{\frac{x^4}{2}} \left( 2 x^3 + \frac{1}{x} \right) w & = & – x^3 e^{\frac{x^4}{2}}\\ x e^{\frac{x^4}{2}} \frac{d w}{d x} + 2 x^4 e^{\frac{x^4}{2}} w + e^{\frac{x^4}{2}} w & = & – x^3 e^{\frac{x^4}{2}}\\ \frac{d}{d x} \left( x e^{\frac{x^4}{2}} w \right) & = & – x^3 e^{\frac{x^4}{2}}\\ \int d \left( x e^{\frac{x^4}{2}} w \right) & = & – \int x^3 e^{\frac{x^4}{2}} d x + C\\ x e^{\frac{x^4}{2}} w & = & – \frac{2}{4} \int \frac{4 x^3}{2} e^{\frac{x^4}{2}} d x + C\\ w & = & – \frac{1}{2 x} + \frac{C}{x} e^{\frac{- x^4}{2}} \end{eqnarray*} $$Regresando a las variables originales:
$$ \begin{eqnarray*} \frac{1}{u} & = & – \frac{1}{2 x} + \frac{C}{x} e^{\frac{- x^4}{2}}\\ \frac{1}{u} & = & \left( \frac{- x + 2 C x e^{\frac{- x^4}{2}}}{2 x^2} \right)\\ \frac{2 x^2}{2 C x e^{\frac{- x^4}{2}} – x} & = & u\\ \frac{x}{C e^{\frac{- x^4}{2}} – \frac{1}{2}} & = & y – x\\ y & = & \frac{x}{C e^{\frac{- x^4}{2}} – \frac{1}{2}} + x \end{eqnarray*} $$Por tanto la solución de la ED de Riccati (y Bernoulli), es:
$$y = \frac{x}{C e^{\frac{- x^4}{2}} – \frac{1}{2}} + x$$

Si quieres aprender a automatizar tus resultados y tener la seguridad de los pasos que estás obteniendo te dejo nuestro recurso: Ecuaciones Diferenciales de Primer Orden Sagemath Python Lineales y No Lineales paso a paso.
Ejercicio 3.
Resolver:
$$y’=-y^{2}\sin{(x)}+2\tan{(x)}\sec{(x)}$$
Suponemos una solución: $y_1=\sec{(x)}$.
Solución.
Paso 1. Forma estándar:
$$y’=-\sin{(x)}y^{2}+2\tan{(x)}\sec{(x)}$$
Paso 2. Sí, es una ED de Riccati, aún cuando no cuenta con el término: $b(x)y$, por tanto transformamos a una ED de Bernoulli.
Tenemos que $y_1=\sec{(x)}$, es una solución conocida de la ED, por tanto:
Paso 3. Primera sustitución con $y=\sec{(x)}+u$, de modo que, $\frac{dy}{dx}=\sec{(x)\tan{(x)}}+\frac{du}{dx}$, de modo que:
$$ \begin{eqnarray*} y’ & = & – \sin(x) y^2 + 2 \tan (x) \sec (x)\\ \sec (x) \tan (x) + \frac{d u}{d x} & = & – \sin(x) (\sec (x) + u)^2 + 2 \tan (x) \sec(x)\\ \frac{d u}{d x} & = & – \sin(x) (\sec(x)^2 + 2 \sec(x) u + u^2) + 2 \tan (x) \sec(x) – \sec (x) \tan(x)\\ \frac{d u}{d x} & = & – \sin(x) \sec(x)^2 – 2 \sin(x) \sec (x) u – \sin(x) u^2 + 2 \tan(x) \sec(x) – \sec(x) \tan(x)\\ \frac{d u}{d x} + 2 \sec (x) \sin(x) u & = & – \sin(x) \sec(x)^2 – \sin(x) u^2 + 2 \tan(x) \sec(x) – \sec(x) \tan(x)\\ \frac{d u}{d x} + 2 \frac{\sin(x)}{\cos (x)} u & = & – \frac{\sin(x)}{\cos (x)^2} – \sin(x) u^2 + 2 \frac{\sin(x)}{\cos (x)^2} – \frac{\sin(x)}{\cos (x)^2}\\ \frac{d u}{d x} + 2 \frac{\sin(x)}{\cos (x)} u & = & – \sin(x) u^2 \end{eqnarray*} $$De modo que obtenemos la ED de Bernoulli:
$$\frac{du}{dx}+2\frac{\sin{(x)}}{\cos{(x)}}u=-\sin{(x)}u^{2}$$
Donde $n=2$, según el algoritmo del artículo: Ecuaciones Diferenciales de Bernoulli.
Segunda sustitución: $u=w^{-1}$ para resolve la ED de Bernoulli, donde, $\frac{du}{dx}=-w^{-2}\frac{du}{dx}$, de modo que:
$$ \begin{eqnarray*} – \frac{1}{w^2} \frac{d w}{d x} + 2 \frac{\sin(x)}{\cos (x)} \left( \frac{1}{w} \right) & = & – \sin(x) \left( \frac{1}{w}\right)^2\\ \frac{d w}{d x} – 2 \frac{\sin(x)}{\cos (x)} w & = & \sin(x) \end{eqnarray*} $$De este modo, como sabemos, obtenemos una ED lineal de primer orden y para resolverla, utilizaremos el algoritmo desarrollado en nuestro artículo: Factores Integrantes. Por tanto, obtenemos el factor integrante:
$$e^{\int{P(x)}dx}$$
Para nuestro caso: $P(x)=-2\frac{\sin{x}}{\cos{x}}$, de modo que:
$$ \begin{eqnarray*} \int P (x) d x & = & – 2 \int \frac{\sin(x)}{\cos (x)} d x\\ \int P (x) d x & = & 2 \int \frac{- \sin(x)}{\cos (x)} d x\\ \int P (x) d x & = & 2 l n (\cos (x)) \end{eqnarray*} $$Es decir, el factor integrante buscado es:
$$ \begin{eqnarray*} e^{\int P (x) d x} & = & e^{2 l n (\cos (x))}\\ e^{\int P (x) d x} & = & e^{l n (\cos (x)^2)}\\ e^{\int P (x) d x} & = & \cos (x)^2 \end{eqnarray*} $$Ésto implica:
$$ \begin{eqnarray*} \cos (x)^2 \left[ \frac{d w}{d x} – 2 \frac{\sin(x)}{\cos (x)} w\right] & = & \cos (x)^2 \sin(x)\\ \cos (x)^2 \frac{d w}{d x} – 2 \sin(x) \cos (x) w & = & \cos(x)^2 \sin(x)\\ \frac{d}{d x} (\cos (x)^2 w) & = & \cos (x)^2 \sin(x)\\ d (\cos (x)^2 w) & = & \cos (x)^2 \sin(x) d x\\ \int d (\cos (x)^2 w) & = & \int \cos (x)^2 \sin(x) d x + C\\ \cos (x)^2 w & = & \int \cos (x)^2 \sin(x) d x + C \end{eqnarray*} $$Ahora, integrando $\int{\cos{(x)}^{2}\sin{(x)}dx}$, (ver el artículo: Factores Integrantes), procedemos de la siguiente forma:
Integramos usando la fórmula: $\int{u^{n}du}=\frac{u^{n+1}}{n+1}$, esto es, $u=\cos{(x)}$, $du=-\sin{(x)}dx$, de modo que:
$$ \begin{eqnarray*} \cos (x)^2 w & = & – \int – \cos (x)^2 \sin(x) d x + C\\ \cos (x)^2 w & = & – \frac{\cos (x)^3}{3} + C \sec (x)^2\\ w & = & – \frac{1}{3} \cos (x) + C \sec (x)^2 \end{eqnarray*} $$Regresando a las variables originales:
$$ \begin{eqnarray*} \frac{1}{u} & = & – \frac{1}{3} \cos(x) + C \sec(x)^2\\ \frac{1}{- \frac{1}{3} \cos (x) + C \sec(x)^2} & = & u\\ u & = & \frac{1}{- \frac{1}{3} \cos (x) + C \sec (x)^2}\\ y – \sec(x) & = & \frac{3}{- \cos(x) + 3 C \sec(x)^2}\\ y & = & \frac{3}{- \cos (x) + 3 C \sec (x)^2} + \sec (x) \end{eqnarray*} $$Por tanto la solución de la ED de Riccati (y Bernoulli), es:
$$y=\frac{3}{-\cos{(x)}+3C\sec{(x)}}+\sec{(x)}$$
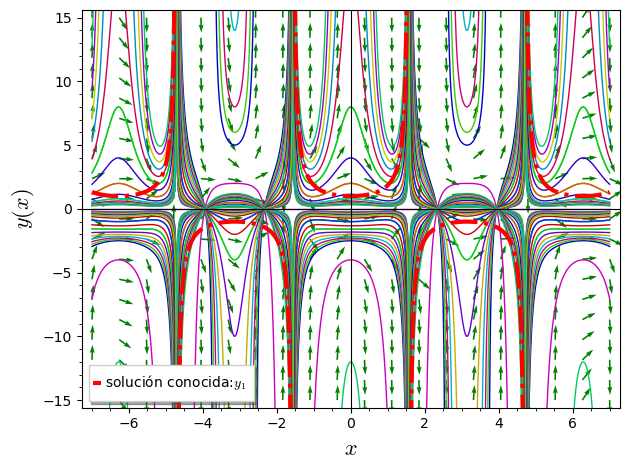
Si quieres aprender a automatizar tus resultados y tener la seguridad de los pasos que estás obteniendo te dejo nuestro recurso: Ecuaciones Diferenciales de Primer Orden Sagemath Python Lineales y No Lineales paso a paso.
Conviertete en un Expert@ en Ecuaciones Diferenciales Lineales y No-Lineales

Ahora que has explorado los conceptos fundamentales de la Ecuación Diferencial de Riccati y has seguido paso a paso la metodología detallada para su resolución, estás en el camino correcto para convertirte en un experto en este fascinante campo de las matemáticas aplicadas, por lo que te recomiendo revises los siguientes ¡Enlaces Importantes!
Recursos especializados:
- Factores Integrantes – Desentraña los secretos detrás de los factores integrantes y mejora tu comprensión de las Ecuaciones Diferenciales.
- Ecuaciones Diferenciales de Bernoulli – Sumérgete en la resolución de Ecuaciones Diferenciales de Bernoulli y descubre las aplicaciones prácticas de esta técnica.
- Resolución Detallada del Problema 15 de Ecuaciones Diferenciales de G. Zill – Accede a una solución detallada del desafiante Problema 15 de Ecuaciones Diferenciales propuesto por G. Zill.
Para llevar tu conocimiento al siguiente nivel, te recomendamos nuestras herramientas y cursos exclusivos:
- Automatiza tus Soluciones: Ecuaciones Diferenciales de Primer Orden Sagemath Python Lineales y No Lineales paso a paso – Simplifica tus resoluciones con códigos prácticos en Python y SageMath.
- Ejercicios_Resueltos_Riccati_SageMath.ipynb. – Domina la resolución de Ecuaciones de Riccati con códigos que te permiten obtener resultados inmediatos, masivos y reales.

Explora Nuestros Cursos Exclusivos:
- ¿Qué son las Ecuaciones Diferenciales? – Adéntrate en los fundamentos de las Ecuaciones Diferenciales y amplía tu perspectiva sobre su aplicabilidad.
- Ecuaciones Diferenciales de Primer Orden – Perfecciona tus habilidades con nuestro curso especializado en Ecuaciones Diferenciales de Primer Orden.
- Programa Completo: Ecuaciones Diferenciales, Modelado, Aplicaciones e Inteligencia Artificial – Descubre nuestro programa integral que abarca Ecuaciones Diferenciales, Modelado, Aplicaciones e Inteligencia Artificial. Un paso crucial hacia tu dominio en este campo.

Nuestros recursos están diseñados para aquellos que buscan alcanzar un nivel excepcional en Ecuaciones Diferenciales (e Inteligencia artificial) y elevarse al pináculo de su sector profesional, así como tambien para docentes y estudiantres comprometidos con su excelencia!. ¡Invierte en tu crecimiento académico y conviértete en un EXPERTO hoy!
¿Encontraste lo que buscabas?
¿Quieres comenzar desde cero? te recomiendo nuestro artículo: Tipos de ecuaciones diferenciales ordinarias de primer orden y su clasificación,
¿Quiero una visión general desde cero? te recomiendo nuestro artículo: Domina las Ecuaciones Diferenciales Ordinarias: Guía Esencial 2024,
¿Quieres ejemplos sobre inteligencia artificial y ecuaciones diferenciales, revisa nuestro artículo: Cómo Resolver Ejercicios de Estimación de Parámetros en Sistemas No Lineales?
¿Quieres más profuncdidad en el conocimiento de las ecuaciones no-lineales de pimer orden? te recomiendo nuestros artículos:



