Ecuaciones diferenciales de variables separables ejemplos resueltos en 3 pasos.
En esta ocasión desarrollo 6 ejemplos de ecuaciones diferenciables de variables separables, partiendo del caso base donde la ecuación se presenta en su forma estándar.
1.- La ecuación diferencial se escribe en la FORMA ESTÁNDAR propia de una ecuación diferencial ordinaria de primer orden:
$\frac{dy}{dx}=f\left ( x,y \right )$
Ejemplo:
$\frac{dy}{dx}=\frac{3x^{2}+4x+2}{2\left ( y-1 \right )}$
Donde:
$f(x,y)=\frac{3x^{2}+4x+2}{2\left ( y-1 \right )}$
2.- SEPARAMOS LAS VARIABLES de acuerdo al criterio visto en el artículo: Cómo resolver una Ecuación Diferencial de primer orden separable
$Mdx = Ndy$
Donde:
$M=f(x)$ y $N=f(y)$
La mnemotecnia utilizada para este paso es: Pájaros de un mismo plumaje vuelan juntos
3.- Por último, INTEGRAMOS ambos miembros de la ecuación mediante las fórmulas y técnicas conocidas de Cálculo integral
#.#.#.#.#.#.##.#.#.#.#.#.##.#.#.#.#.#.##.#.#.#.#.#.##.#.#.#.#.#.##.#.#.#.#.#.##.#

Ejemplo 1:
I. $\frac{dy}{dx}=\frac{3x^{2}+4x+2}{2\left ( y-1 \right )}$
Pasos:
1.- $\frac{dy}{dx}=\frac{3x^{2}+4x+2}{2\left ( y-1 \right )}$
2.- $2\left ( y-1 \right )dy=\left ( 3x^{2}+4x+2 \right )dx$
$\Rightarrow 2ydy-2dy=3x^{2}dx+4xdx+2dx$
3.- $\Rightarrow 2\int ydy – 2\int dy=3\int x^{2}dx+4\int xdx+2\int dx+C$
$\Rightarrow \frac{2}{2}y^{2}-2y=\frac{3}{3}x^{3}+\frac{4}{2}x^{2}+2x+C$
Resultado:
$\Rightarrow y^{2}-2y=x^{3}+2x^{2}+2x+C$
IMPORTANTE, en esta ocasión los resultados los representaré implícitamente; es decir, no despejaré la variable dependiente, lo cual en realidad es un problema de álgebra o mejor aún, de métodos numéricos.
Ejemplo 2:
II. $\frac{dy}{dx}=\frac{y\cos x}{1+2y^{2}}$
Pasos:
1.- $\frac{dy}{dx}=\frac{y\cos x}{1+2y^{2}}$
2.- $\left ( 1+2y^{2} \right )dy=y\cos xdx$
$\Rightarrow \frac{\left ( 1+2y^{2} \right )dy}{y}=\cos xdx$
$\Rightarrow \frac{1}{y}dy+2ydy=\cos xdx$
3.- $\int \frac{dy}{y}+2\int ydy=\cos xdx+C$
$\Rightarrow \ln y+\frac{2}{2}y^{2}=\sin x+C$
Resultado:
$\Rightarrow \ln y+y^{2}=\sin x+C$
Ejemplo 3:
III. $\frac{dy}{dx}=\frac{x^{2}}{1-y^{2}}$
Pasos:
1.- $\frac{dy}{dx}=\frac{x^{2}}{1-y^{2}}$
2.- $\left ( 1-y^{2} \right )dy=x^{2}dx$
$\Rightarrow dy-y^{2}dy=x^{2}dx$
3.- $\int dy-\int y^{2}dy=\int x^{2}dx+C$
Resultado:
$y-\frac{1}{3}y^{3}=\frac{1}{3}x^{3}+C$
Ejemplo 4:
IV. $x\frac{dy}{dx}=4y$
Pasos:
1.- $x\frac{dy}{dx}=4y$
2.- $xdy=4ydx$
$\frac{1}{4}\frac{dy}{y}=\frac{dx}{x}$
3.- $\frac{1}{4}\int \frac{dy}{y}=\int \frac{dx}{x}+C$
$\Rightarrow \frac{1}{4}\ln y=\ln x+C$
$\Rightarrow \ln y^{1/4}=\ln x+C$
$\Rightarrow e^{\ln y^{1/4}}=e^{\ln x+C}$
$\Rightarrow y^{1/4}=e^{\ln x}e^{C}$
Resultado:
$y^{1/4}=C_{1}x$
Se puede simplificar con álgebra quedando:
$\Rightarrow \left ( y^{1/4} \right )^{4}=\left ( C_{1}x \right )^{4}$
$\Rightarrow y=C_{2}x^{4}$
La gráfica de la función es:

Ejemplo 5:
V. $\frac{dy}{dx}=y\sin x$
Pasos:
1.- $\frac{dy}{dx}=y\sin x$
2.- $\frac{dy}{y}=\sin xdx$
3.- $\int \frac{dy}{y}=\int \sin xdx+C$
$\Rightarrow \ln y=-\cos x+C$
$\Rightarrow e^{\ln y}=e^{-\cos x+C}$
$y=e^{-\cos x+C}$
$y=e^{-\cos x}e^{C}$
Resultado:
$y=C_{1}e^{-\cos x}$
La gráfica de la función es:
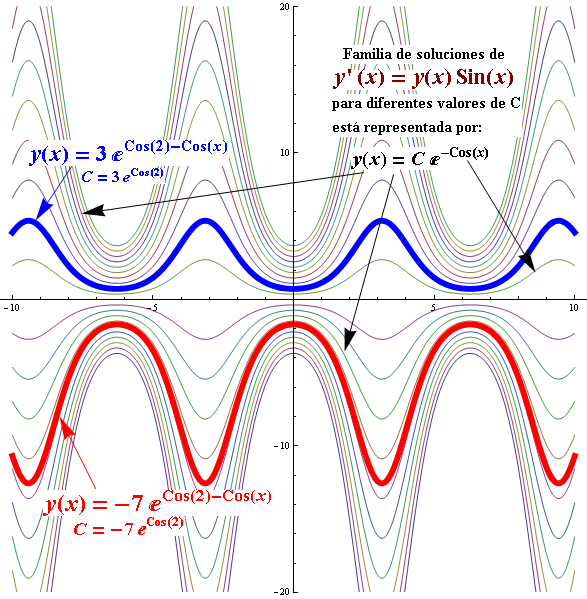
Código de MATHEMATICA para el problema 5
Clear["Global`*"]
(*Solución general del sistema no Homogéneo*)
sol = DSolve[y'[x] == y[x] Sin[x], y[x], x] // Expand
(*Solución Particular 1 del sistema no Homogéneo*)
sol1 = DSolve[{y'[x] == y[x] Sin[x], y[2] == 3}, y[x], x] // Expand
(*Solución Particular 2 del sistema no Homogéneo*)
sol2 = DSolve[{y'[x] == y[x] Sin[x], y[-2] == -7}, y[x], x] // Expand
(*Familia de Soluciones del sistema NO Homogéneo*)
sols = Table[Evaluate[sol[[1, 1, 2]] /. C[1] -> i], {i, -10, 10}];
(*GRAFICA DE SOLUCIONES DEL SISTEMA NO HOMOGÉNEO*)
(*Familia de Soluciones*)
pfsnh = Plot[sols, {x, -10, 10}, PlotRange -> {-20, 20},
AspectRatio -> 1];
(*Solución Particular1*)
pspsnh = Plot[sol1[[1, 1, 2]], {x, -10, 10}, PlotRange -> {-20, 20},
AspectRatio -> 1, PlotStyle -> {Blue, Thickness[0.01]}];
(*Solución Particular2*)
pspsnh2 =
Plot[sol2[[1, 1, 2]], {x, -10, 10}, PlotRange -> {-20, 20},
AspectRatio -> 1, PlotStyle -> {Red, Thickness[0.01]}];
Show[pfsnh, pspsnh, pspsnh2]
Para que obtengas la confianza necesaria te recomendamos, nuestro programa:

Ecuaciones Diferenciales Aplicaciones e IA
Encontraste la información que buscabas?
No, necesito un ejemplo más (da click aquí)
Te invito a que me contactes aquí para cualquier sugerencia sobre la página y si tienes una duda en particular sobre el tema tratado, por favor, deja tu comentario al final de esta página. Que estés bien. 😉

muy buena la información, pero no tiene la opción para descargar la información, como podría hacer??? me pueden ayudar!!!
Hola Frank
Este artículo lo escribí directamente en el Blog, por lo que no tengo el archivo en algún procesador de texto, sin embargo hay una solución sencilla.
Utiliza la barra flotante para compartir («AddThis o share»):
share_bar
y da un click en la opción imprimir, que es el ícono: Icono imprimir
para seleccionar la opción de impresión o GUARDADO que gustes (te sugiero, guardar como PDF).
El archivo que guardarás o imprimiras se verá asi:
Opción de impresión de artículos del blog utilizando la barra de «share» (solo muestro una parte de lo que podrás guardar en esta imagen, pero el artículo se guarda o imprime completo)
Espero te ayude.
Saludos
hola tengo un problema con un ejercicio de variable separable es xe elevado ala x y esta misma x – y pero la x elevada esta elevada ala 2 por favor necesito una ayuda
Hola adraina, te agradecería escribieras la ecuación diferencial acá en los comentarios, no es clara la configuración de la misma.
Podría ser:
$\int xe^{x}(x^{2} – y)dx$?
O cual es la ed?
No te preocupes si no la puedes escribir en LaTeX, solo escribela, ok?
Saludos
quisiera una ayuda con:
secxdy’ + (csc(y2))/y = 0
Hola Adriana, aquí te dejo la solución:
Problema resuelto para el Blog:
${Sec} (x) y’ + \frac{Csc(y^2)}{y} = 0$
Solución:
En este caso se trata de una:
Ecuación Diferencial No lineal de primer orden
${Sec} (x) \frac{d y}{d x} + \frac{{Csc} (y^2)}{y} = 0$
$\frac{d y}{d x} = – \frac{{Csc} (y^2)}{y} \ast \frac{1}{{Sec} (x)}$
$\frac{d y}{d x} = – \frac{{Csc} (y^2) {Cos} (x)}{y}$
-Separando variables:
$\frac{y}{{Csc} (y^2)} \frac{d y}{d x} = – {Cos} (x)$
${Sen} (y^2) y d y = – {Cos} (x) d x$
Integramos:
$\int {Sen} (y^2) y d y = – \int {Cos} (x) d x + C$
-Recordamos las formulas de integración:
$\int u^{n} d u = \frac{u^{n + 1}}{n + 1}$ y
$\int {Sen} u d u = – {Cos} u + C$
-Por tanto, si:
$u = y^2$ $\Rightarrow$ $d u = 2 y d y$, de donde:
$\int {Sen} (y^2) y d y = \frac{1}{2} \int {Sen} (y^2) (2) y d y =\frac{1}{2} {Cos} (y^2) + C$
-De modo que, regresando a:
$\int {Sen} (y^2) y d y = – \int {Cos} (x) d x + C$
-Tenemos:
$\frac{1}{2} \int {Sen} (y^2) (2) y d y = – \int {Cos} (x) d x + C$
$\frac{1}{2} {Cos} (y^2) = – {Sen} (x) + C$
Por tanto el resultado buscado en forma implícita es:
$-\frac{1}{2} {Cos} (y^2) = – {Sen} (x) + C$
-Y de forma explicita:
$- \frac{1}{2} {Cos} (y^2) = – {Sen} (x) + C$
${Cos} (y^2) = 2 {Sen} (x) + 2 C$
$y^2 = {Cos}^{- 1} (2 {Sen} (x) + C_1)$
$y = \pm \sqrt{{Cos}^{- 1} (2 {Sen} (x) + C_1)}$
Saludos. 😉
Una pregunta… que pasa si es una EDO de variable separable y tienee tbn una funcion q no depende de y… no se si me explico… una mezcla entre EDO SEPARABLE Y DE VARIABLE SEPARADA
Hola Juan
Podrías poner un ejemplo? no se si te refieras a una ED lineal; un ejemplo de éstas sería:
${{y}^{‘}}+3{{x}^{2}}y={{x}^{2}}$
La solución para este tipo de ecuaciones la puedes ver en el siguiente enlace:
Ecuacion diferencial lineal ejercicios resueltos. Libro: Dennis G. Zill 7ª Ed. Capítulo 2.3 (1-5)
El método de solución, lo desarrollo en este artículo:
CÓMO RESOLVER ECUACIONES DIFERENCIALES CON EL MÉTODO DEL FACTOR INTEGRANTE. MÉTODO DE 4 PASOS
Espero aclare tu duda, si no, por favor, escribe un ejemplo. Puedes?
Un saludo. =)
una ayudita con este problema xydx-(x+2)dy=0
Que tal maicol
Me imagino que la dificultad está en la integración de la función racional.
Para esta te sugiero hagas lo siguiente cuando te enfrentes a una de estas:
1.- si el GRADO del numerador es mayor o igual que el del denominador, realiza una división de polinomios (que es lo que hice en éste caso)
2.- Si es menor, puede haber varios casos: a). puede ser del tipo $\int{\frac{dT}{T}}$
b). puede ser mediante Fracciones parciales
c). puede ser mediante adecuarlas a alguna formula de integración
Para tu caso, te dejo la solución:
$x y {dx} – (x + 2) {dy} = 0$
$\Rightarrow x y {dx} = (x + 2) {dy}$
$\Rightarrow \frac{x {dx}}{x + 2} = \frac{{dy}}{y}$
$\Rightarrow \left( 1 – \frac{2}{x + 2} \right) {dx} = \frac{{dy}}{y}$
$\Rightarrow \int \left( 1 – \frac{2}{x + 2} \right) {dx} = \int\frac{{dy}}{y} + C$
$\Rightarrow \int {dx} – 2 \int \frac{{dx}}{x + 2} = \int\frac{{dy}}{y} + C$
$\Rightarrow x – 2 \ln | x + 2 | = \ln | y | + C$
$\Rightarrow x – \ln (x + 2)^2 = \ln | y | + C$
$\Rightarrow x + C_1 = \ln (x + 2)^2 + \ln | y |$
$\Rightarrow x + C_1 = \ln [ (x + 2)^2 y]$
$\Rightarrow C_2 e^x = (x + 2)^2 y$
Por tanto:
$y (x) = \frac{C_2^{} e^x}{(x + 2)^2}$
excelente ing que realice las dudad que tiene uno como estudiante la verdad yo soy bueno en las matematicas pero ecuaciones diferenciales me estoy matando la cabeza
Hola nacional
Te sugiero, si me permites, que emplees las técnicas analíticas y/o numéricas para corroborar tus resultados cualitativos, asumiendo que es la parte que te genera problemas. De otra forma, te sugiero qeu emplees las técnicas y luego las razones; y si llegas a un punto donde no puedes avanzar, dejes un rato tu trabajo y te dediques a otra cosa un poco más relajante de preferencia.
Lee el siguiente artículo: Como aprender Ecuaciones Diferenciales
Para abordar las técnicas numéricas y simular numéricamente tus ED’s empieza por acá (dale click al enlace): Método de Euler
Para simular tus ED’s con software en esta misma página en tiempo real, dale click al siguiente enlace: Simulación con SAGE
Saludos
buenas necesito de su ayuda en un problema de separación de variable dy/(dx )-ysenx=0 para y(π/2)=0
Hola Rigoberto,
Te dejo la respuesta:
PVI:
$\frac{{dy}}{{dx}} – y {sen} (x) = 0$; sujeta a: $y \left(\frac{\pi}{2} \right) = 2$
Solución:
$\frac{{dy}}{{dx}} = y {sen} (x)$
$\frac{{dy}}{y} = {sen} (x) {dx}$
Integrando:
${Ln} (y) = – \cos (x) + C$
$y = e^{- \cos (x) + C}$
$y = C_1 e^{- \cos (x)}$
Para encontrar $C_{1}$, sustituímos,
los valores iniciales:
$2 = C_1 e^{- \cos \left( \frac{\pi}{2} \right)}$
$2 e^{\cos \left( \frac{\pi}{2} \right)} = C_1$
$C_1 = 2 e^0$
$C_1 = 2 (1)$
$C_1 = 2$
Por tanto la solución particular buscada es:
$y = 2^{} e^{- \cos (x)}$
hola tengo tengo un problema con este ejericicio de variables separables
sin(3x)dx + 2ycos3(3x)dy = 0
Hola Marcela
Disculpa el que no haya podido atenderte antes.
Aquí te dejo la respuesta:
La respuesta es:
$$\sin (3 x) + 2 {ycos} (3 x) \frac{{dy}}{{dx}} = 0$$
$$\frac{{dy}}{{dx}} = \frac{- \sin (3 x)}{2 y \cos (3 x)}$$
$$\frac{{dy}}{{dx}} = \frac{- \tan (3 x)}{2 y}$$
Separando variables:
$$2 y \frac{{dy}}{{dx}} = – \tan (3 x)$$
$$2 y {dy} = – \tan (3 x) {dx}$$
Integrando:
$$2 \int y {dy} = – \int \tan (3 x) {dx} + C$$
$$2 \int y {dy} = – \frac{1}{3} \int \tan (3 x) (3) {dx} + C$$
$$y^2 = \frac{1}{3} \ln (\cos (3 x)) + C$$
Por lo que el resultado es:
$$y = \sqrt{\frac{1}{3} \ln (\cos (3 x)) + C}$$
La formula de integración que utilice es:
$$\int {Tan} x {dx} = – \ln (\cos x) + C$$
Saludos
mi duda es sobre tgx.(sen(y)^2)dx+(cosx^2).ctg(y)dy=0
Hola Sergio, te dejo la respuesta.
Respuesta:
$${Tg} (x) {Sen}^2 (y) {dx} + {Cos}^2 (x) {Ctg} (y){dy} = 0$$
Separando Variables:
$${Tg} (x) {Sen}^2 (y) {dx} = – {Cos}^2 (x) {Ctg} (y){dy}$$
$$\frac{{Tg} (x)}{- {Cos}^2 (x)} {dx} = \frac{{Ctg}(y)}{{Sen}^2 (y)} {dy}$$
$$\Rightarrow – {Tg} (x) {Sec}^2 (x) {dx} = {Ctg} (y){Csc}^2 (y) {dy}$$
Ahora, sabemos que si:
$$f (x) = {Tg} (x) \Rightarrow f’ (x) = {Sec}^2 (x)$$ y
$$f (x) = {Ctg} (x) \Rightarrow f’ (x) = {Csc}^2 (x)$$
Por tanto, utilizando la fórmula:
$$\int x^n {dx} = \frac{x^{n + 1}}{n + 1}$$, por tanto:
$$- \int {Tg} (x) {Sec}^2 (x) {dx} = \int {Ctg} (y){Csc}^2 (y) {dy} + C_1$$
$$\Rightarrow – \frac{{Tg}^2 (x)}{2} = \frac{{Ctg}^2 (y)}{2} + C_1$$
Mediante algebra:
$$\Rightarrow – {Tg}^2 (x) = {Ctg}^2 (y) + 2 C_1$$
$$\Rightarrow {Ctg}^2 (y) = – {Tg}^2 (x) – 2 C_1$$
$$\Rightarrow 2 C_1 = – {Tg}^2 (x) – {Ctg}^2 (y)$$
Por tanto el resultado es:
$$C = – ({Tg}^2 (x) + {Ctg}^2 (y))$$
Saludos
Que tal, tengo una duda con la ecuación raiz cuadrada de 1 menos y cuadrada eso multiplicado por dx menos la raiz cuadrada 1 menos x cuadrada eso por dy igual con cero
Hola Gabriel, disculpa la demora
Aquí tienes la explicacion paso a paso
Respuesta:
$$\sqrt{1 – y^2} {dx} = \sqrt{1 – x^2} {dy}$$
Resolviendo por variables separables:
$$\frac{{dx}}{\sqrt{1 – x^2}} = \frac{{dy}}{\sqrt{1 – y^2}}$$
Integrando:
$$\int \frac{{dy}}{\sqrt{1 – y^2}} = \int \frac{{dx}}{\sqrt{1 – x^2}}$$
Utilizando la fórmula de integración:
$$\int \frac{{dT}}{\sqrt{1 – T^2}} = {arc} \sin T + C$$
Tenemos:
$${arc} \sin y = {arc} \sin x + C$$
$$\Rightarrow y (x) = \sin ({arc} \sin x + C)$$
Por lo que el resultado es:
$$y (x) = \sin ({arc} \sin x + C)$$
Saludos
hola buenas tardes.. me puedes hacer el favor de ayudarme con este ejercicio
)
dy/dt +e»t-y= 0
Diana la solución es la siguiente
$$\frac{{dy}}{{dx}} + e^{t – y} = 0$$
Solución:
$$\frac{{dy}}{{dx}} + e^t e^{- y} = 0$$
$$\frac{{dy}}{{dx}} = – e^t e^{- y}$$
Separando variables
$$\frac{{dy}}{e^{- y}} = – e^t {dt}$$
$$e^y d y = – e^t d t$$
$$\int e^y d y = – \int e^t d t + C$$
$$e^y = – e^t + C$$
Por ultimo, aplicando logaritmos,
obtenemos el resultado:
$$y (t) = {Ln} (- e^t + C)$$
Saludos
Buenas! ¿Cómo sé qué método emplear apropiadamente?, tengo esa duda. Ya que algunas ecuaciones diferenciales se pueden resolver, por ejemplo, el método de las exactas. o similares. Qué debo ver explícitamente para ello, para las otras lo tengo bien claro. Gracias
Christian
El criterio que generalmente sigo yo, es:
1.- escribes la ED en la forma $\frac{dy}{dx}=f(x,y)$ primero
2.- luego descartas la posibilidad de que sean:
a. Separable (o Separable por sustitución)
b. Lineal de 1er orden: la cual lo puede saber de la notación en su forma estándar (buscar la forma estándar aquí en el apartado de «Metodo de 4 pasos para resolver …»
– De Bernoulli: mediante su forma estándar (busca la forma estandar en la metodología de 4 pasos aquí)
– De Ricatti: mediante su forma estándar
c.- Homogenea: criterio de homogeneidad (busca dicho criterio aquí)
d.- Exacta: criterio de exactitud (busca dicho criterio aquí)
e.- No lineal: Mediante su forma estándar y recurriendo a los dos puntos que
determinan la linealidad de una ED. (Ejemplos sobre la forma estándar de la ecuación logística los encuentras aquí)
Las ED que se resuelven por sustitución son amplias (aunque simplemente son ED’s separables, lo cual es divertido a fin de cuentas =) ) enfocate en principio en las que se presentan mas en los libros de texto -donde la sustitución es algo como $u = x + y$ y clasificalas (o simplemente ten en cuenta cómo se escribe, en forma estándar, viendo cual es la sustitución adecuada para las mismas y su método de solución – son separables pero la integración resultante puede realizarse mediante fracciones parciales o cualquier otro método de integración, a esto me refiero).
Una vez que adquieras la capacidad para diferenciar éstas ED’s que te describo, se te hará fácil, muy sencillo, clasificar y resolver una Ecuacion diferencial de cualquier orden, mediante métodos analíticos cuando la veas, si vas relacionando las formas estándar de cada tipo y su método de solución, enfocate en las estrategias de solución más comunes para los diferentes tipos de las ED’s.
Por ejemplo:
ED’s de orden 2 pueden ser: Homogéneas y No Homogeneas resolviendolas mediante el método de coeficientes indeterminados;
Sistemas de ED’s pueden ser: acoplados, parcialmente desacoplados y autónomos mediante el método de eigenvalores y igenvectores.
Básicamente todas las ED’s se dividen en lineales y no lineales sean sistemas o ecuaciones individuales.
De modo que puedes iniciar una clasificación con ésta información empezando con estos criterios ya en mente, con el cual fácilmente podrás identificar gran numero de ED’s, te parece?
Espero te sirva esta orientación.
Un saludos afectuoso
hola buenas tardes.. me puedes hacer el favor de ayudarme con este ejercicio
y’= 2x/(y+x^2*y) y(o)= -2
Hola daieni
Aqui está la respuesta:
Resolver el PVI
$y’ = \frac{2 x}{y + x^2 y}$, $y (0) = – 2$
Respuesta:
Paso 2. Separamos variables
$$y’ = \frac{2 x}{y (1 + x^2)}$$
$$y y’ = \frac{2 x}{1 + x^2}$$
$$y \frac{d y}{d x} = \frac{2 x}{1 + x^2}$$
$$y d y = \frac{2 x d x}{1 + x^2}$$
Integramos:
$$\int y d y = \int \frac{2 x d x}{1 + x^2} + C$$
$$u = 1 + x^2$$
$${du} = 2 x d x$$
Por tanto:
$$\int y d y = \int \frac{{du}}{u} + C$$
Implica:
$$\frac{y^2}{2} = \ln u + C$$
Sustituyendo de regreso:
$$\frac{y^2}{2} = \ln (1 + x^2) + C$$
$$y^2 = 2 \ln (1 + x^2) + 2 C$$
$$y = \sqrt{2 \ln (1 + x^2) + C_1}$$
Ahora, resolviendo el PVI:
$$- 2 = \sqrt{2 \ln (1 + (0)^2) + C_1}$$
$$- 2 = \sqrt{C_1}$$
$$C_1 = (- 2)^2$$
$$C_1 = 4$$
De modo que el resultdo es:
$$y_1 = \sqrt{2 \ln (1 + x^2) + 4}$$
$$y_2 = – \sqrt{2 \ln (1 + x^2) + 4}$$
Saludos y suerte 😉
Hola..
Necesito ayuda para comprender porque en una ecuacion como esta..
sec^2 xdy + cscy dx=0 igualo—->sec^2 xdy = -cscy dx
Pero no entiendo el paso siguiente donde al juntar las x con las x y las y con las y
termina con esto….. sen y dy = -con^2 x dx
Debe ser alguna propiedad nose..
Podrias explicarme o indicar algun texto donde lo expliquen
Hola Josue,
Efectivamente, es por las siguientes identidades trigonométricas:
$$\sec{x} = \frac{1}{\cos{x}}$$ y
$$\csc{y} = \frac{1}{\sin{y}}$$
De modo que, sustituyendo en la ED:
$$\sec^{2}{x} dy = – \csc{y} dx$$
$$\rightarrow \frac{1}{\cos{x}}^{2} dy = – \frac{1}{sin{y}} dx$$
$$ \rightarrow \sin{y} dy = – \cos^{2}{x} dx $$
Como vez?
Saludos
Excelnte gracias
De nada Josue.
Saludos
buenas tardes tengo una duda con respecto a un ejercicio.
dy xˆ2 yˆ2
—- = ———–
dx 1+x
espero me puedas ayudar muchas gracias, la pagina y los ejercicios han sido de muchas ayuda.
Que tal Jesus.
Te dejo el resultado de tu ejercicio
Resolviendo
$$\frac{{dy}}{{dx}} = \frac{x^2 y^2}{1 + x}$$
Separamos variables
$$\frac{{dy}}{y^2} = \frac{x^2}{1 + x}$$
El lado izquierdo se resuelve con la fórmula:
$$\int u^n {du} = \frac{u^{n + 1}}{n + 1}$$
El lado derecho, puesto que es una función racional donde el numerador es de mayor grado que el denominador, recurrimos a la división de polinomios
$$\frac{x^2}{x + 1} = x – 1 + \frac{1}{x + 1}$$
De modo que la ED se puede esccribir como:
$$y^{- 2} d y = x – 1 + \frac{1}{x + 1}$$
e integrando
$$\int y^{- 2} d y = \int \left( x – 1 + \frac{1}{x + 1} \right) d x$$
$$\int y^{- 2} d y = \int x d x – \int d x + \int \frac{d x}{x + 1} + C$$
este resulta en:
$$-\frac{1}{y} = \frac{x^2}{2} – x + {Ln} | x + 1 | + C$$
O, despejando $y$:
$$y = – \frac{2}{x^2 – 2 x + 2 C + 2 {Log} (1 + x)}$$
Saludos
que tal buenas tardes ¿podria ayudarme con la ecuación
dy/dx =(1+y^2)tangx; y(0)=1
saludos.
lobo, una disculpa publique tu respuesta hace un par de días en un artículo:
por favor revisa el Ejemplo 1 del siguiente enlace: Ecuaciones diferenciales separables
Saludos
hola podra ayudarme con estos ejercicios por favor
2y(x+1)+y´=0 con y(-2)=1 y=Ce-(x+1)^2
2xyy´=x2+y2 con y(1)=3 y2=x2- Cx
Zahid, para la ED:
$2 y (x + 1) + y’ = 0$; $y (- 2) = 1$
Aqui la respuesta:
$$\Rightarrow \frac{dy}{dx} = – 2 y (x + 1)$$
$$\Rightarrow \frac{dy}{y} = – 2 (x + 1) dx$$
$$\Rightarrow \int \frac{dy}{y} = – 2 \int (x + 1) dx$$
$$\Rightarrow \int \frac{dy}{y} = – 2 \int x dx – 2 \int dx + C$$
$$\Rightarrow Ln (y) = – \frac{2 x^2}{2} – 2 x + C$$
$$\Rightarrow y = e^{- x^2 – 2 x + C}$$
$$\Rightarrow y = C_1 e^{- x^2 – 2 x}$$
$$\Rightarrow y = C_1 e^{- (2 x + x^2)}$$
Resolviendo el PVI:
$$y (- 2) = 1$$
$$\Rightarrow 1 = C_1 e^{- (2 (- 2) + (- 2)^2)}$$
$$\Rightarrow 1 = C_1 e^{- (- 4 + 4)}$$
$$\Rightarrow 1 = C_1 e^{- (0)}$$
$$\Rightarrow 1 = C_1 (1)$$
$$C_1 = 1$$
Por tanto la solución buscada es:
$$y (x) = e^{- (2 x + x^2)}$$
Para el 2o problema:
$2 y y’ = x^2 + y^2$; $y(1)=3$
Es una Ecuación Diferencial de Bernoulli,
que es evidente al ponerla en forma estandar
$$2 y y’ = x^2 + y^2$$
$$\Rightarrow y’ = \frac{x^2 + y^2}{2 xy}$$
$$\Rightarrow y’ = \frac{x^2}{2 x y} + \frac{y^2}{2 x y}$$
$$\Rightarrow y’ = \frac{x}{2 y} + \frac{y}{2 x}$$
$$\Rightarrow y’ – \frac{y}{2 x} = \frac{x}{2 y}$$
$$\Rightarrow y’ – \frac{y}{2 x} = \frac{1}{2} x y^{- 1}$$
Para resolver este tipo de ecuaciones
sigue los cuatro pasos que encontrarás en el siguiente artículo:
Ecuaciones Diferenciales de Bernoulli
El resultado es:
$$y = \sqrt{x} \sqrt{8 + x}$$
Saludos
Hola tengo problemas con estas ecuaciones, realmente no se como solucionarlas
Hola Edward
Las ED’s separables probablemente sean las mas sencillas a resolver si se comienzan con ED’s de primer orden ordinarias.
Solo debes de escribirlas en forma estándar:
El criterio es generalmente es:
1.- Primero, escribes la ED en la forma $\frac{dy}{dx}=f(x,y)$
2.- Luego, revisa que agrupando las variables del mismo tipo en un solo miembro de las ED, es posible.
Ejemplo:
$\frac{dy}{dx}=g(x)h(y)$ $\Rightarrow$ $\frac{dy}{h(y)}=g(x)dx$
O, si se trata de una función racional:
$\frac{dy}{dx}=\frac{g(x)}{h(y)}$ $\Rightarrow$ $h(y)dy=g(x)dx$
Siendo $h(y)$ y $g(x)$ funciones dependientes de la variable independiente $x$
3.- Por últimno, integras según las regras de integración.
Ejemplo:
$\frac{dy}{h(y)}=g(x)dx$ $\Rightarrow$ $\int \frac{dy}{h(y)}= \int g(x)dx+C$
O, en el segundo caso:
$h(y)dy=g(x)dx$ $\Rightarrow$ $\int h(y)dy= \int g(x)dx+C$
Para integrar funciones racionales dificiles, puedes seguir los pasos que aparecen en el siguiente artículo: Ecuaciones Diferenciales Aplicadas. Modelos No lineales, busca el apartado: «Integración de funciones racionales», que está dentro del subtítulo: RESOLVIENDO LA ECUACION DIFERENCIAL NO LINEAL.
Que estes bien.
Edward, no olvides darle like a la fanpage de facebook, ok? Te agradezco de antemano. (y)
GRACIAS ESTOS DOS EJERCICIOS SE ME DIFICULTA RESPONDERLOS
(3x^2+2〖xy〗^2-2x)dx+(3y^2+2x^2 y-2y)dy=0
(2xy-e^2y )dx+(x^2+〖xe〗^2y-y)dy=0
Que tal Eduardo
Te respondo en tu comentario anterior. Más abajo, ok?
Revisalo.
(3x^2+2〖xy〗^2-2x)dx+(3y^2+2x^2 y-2y)dy=0
tengo problemas copn esta ecuacion, me podría ayudar a resolverla
Que tal Eduardo

Con mucho gusto te ayudo, pero necesito lo siguiente:
1. Que tema estas viendo?
2. Me lo envias? la direccion de correo es: ecuaciondiferencialavr@gmail.com
3. En caso de algun error:
a. Revisaste que esten bien copiados los ejercicios?
Estos es lo que interpreto de los ejercicios pedidos:
1.-
2.-
Abre las imagenes en una ventana aparte para verlas mejor en caso que lo necesites y corroborar si esos son los ejercicios que quieres resolver. Si es así, no olvides enviarme los temas que estas viendo a el correo que te deje más arriba.
Si muchas gracias, al final si los pude resolver y si están bien copiados solo que no se como subirlos con ese formato, lo revisaré para en eventos futuros no errar, aun así muchas gracias seguiré en contacto contigo para aclarar mis dudas, te deseo buenas noches, continuamos en contacto.
Saludos desde Santiago de Querétaro.
me podrias ayudar con este problema
(1+x^2)dy/dx = 1+y^2
katerine
La respuesta es:
$$(1+x^2)\frac{dy}{dx}=1+y^{2}$$
$$\frac{dy}{1+y^{2}}=\frac{dx}{1+x^{2}}$$
$$\int \frac{dy}{1+y^{2}}=\int \frac{dx}{1+x^{2}}$$
Usando:
$$\int \frac{dT}{1+T^{2}}=\arctan{T}+C$$
Por tanto:
$$\int \frac{dy}{1+y^{2}}=\int \frac{dx}{1+x^{2}} + C$$
$$\rightarrow \arctan( y )= \arctan( x )+ C$$
$$\rightarrow y = \tan{(\arctan( x )+ C)}$$
Saludos
ayudita porfis
(e^y+1)cosxdx+e^y(senx+1)dy=0
Hola stephani
Aquí esta la respuesta.
Tenemos:
$$(e^y + 1) Cos(x)dx + e^y (Sen(x) + 1)dy = 0$$
Forma estandar:
$$\frac{dy}{dx} = – \frac{(e^y + 1)Cos(x)}{e^y(Sen(x) + 1)}$$
Es una ED Separable.
De moque que procedemos como lo sugiere éste artículo
$$\frac{e^y}{(e^y + 1)}dy = – \frac{Cos(x)}{Sen(x) + 1}dx$$ ….. (1)
Utlizamos:
$\int u^n du = \frac{u^{n + 1}}{n + 1}$
Donde, lado izquierdo:
$u = e^y + 1$
$du = e^y dy$
y, lado derecho:
$v = Sen(x) + 1$
$d v = Cos(x) dx$
Integrando (1):
$$\int \frac{e^y}{(e^y + 1)}dy = – \int \frac{Cos(x)}{Sen(x) + 1}dx + C$$
$$Ln (e^y + 1) = – Ln (Sen (x) + 1) + C$$
$$Ln (e^y + 1) = Ln \left( \frac{1}{Sen (x) + 1} \right) +C$$
$$e^y + 1 = e^{Ln \left( \frac{1}{Sen (x) + 1} \right) + C}$$
$$e^y + 1 = \frac{1}{Sen (x) + 1} \ast e^C$$
$$e^y + 1 = \frac{C_1}{Sen(x) + 1}$$
$$e^y = \frac{C_1}{Sen(x) + 1} – 1$$
Por tanto:
$$y = Ln \left( \frac{C_1}{Sen(x) + 1} – 1 \right)$$
Saludos
Saludos…
Please
Ayuda con estos ejercicios
(x+√y^2-xy)dx/dy=y, cony (1)=1
(x – y cos(y/x))dx + x cos(y/x)dy = 0
Katherin, no entiendo la ED del PVI
La segunda, es decir $(x – y\cos{\frac{y}{x}})dx+x\cos{\frac{y}{x}}dy$
se resuelve utilizando la sustitución $u(x) = \frac{y}{x}$, no tengo tiempo de momento para desarrollarla, espero que eso te sirva, mañana te escribo mas pasos, para que te guies, saludos
hola Buenas Tardes maestro estar por ahi
quisiera que me ayudara con un ejercicio ya lo hice pero quisiera saber si lo he realizado bien ya que significa 1 punto para mis notas parciales
el ejercicios es el siguiente
x^2y^2dy=(y+1)dx
me podria ayudar con ese ejercicio
Hola Jose
Te dejo la respuesta
Tenemos:
$$x^2 y^2 dy = (y + 1) dx$$
Solución:
Forma estándar:
$$\frac{dy}{dx} = \frac{y + 1}{x^2 y^2}$$
Separando variables:
$$\frac{y^2}{y + 1} dy = \frac{dx}{x^2}$$
Simplificando la función racional: $\frac{y^2}{y + 1}$
Mediante la division de polinomios, vemos que:
$$\frac{y^2}{y + 1} = y – 1 + \frac{1}{y + 1}$$
Por tanto:
$$\frac{y^2}{y + 1} dy = \frac{dx}{x^2}$$
Implica:
$$\left( y – 1 + \frac{1}{y + 1} \right) dy = \frac{dx}{x^2}$$
$$\Rightarrow y dy + dy + \frac{dy}{y + 1} = \frac{dx}{x^2}$$
Integrando:
$$\int y dy + \int dy + \int \frac{dy}{y + 1} = \int \frac{dx}{x^2} + C$$
$$\frac{y^2}{2} + y + Ln (y + 1) = – \frac{1}{x} + C$$
De modo que el resultado implicito es:
$$C = \frac{1}{x} + \frac{y^2}{2} + y + Ln (y + 1)$$
Puedes, incluso, despejar la $x$, para un resultado explícito.
Saludos
podria ayudarme con esta ecuacion
y’+y tanx=o
Hola alan
Te dejo la solución
Tenemos:
$$y’ + y Tan (x) = 0$$
Paso 1: Forma estándar
$$y’ = – y Tan (x)$$
$$\frac{dy}{dx} = – y Tan (x)$$
Paso 2: Separamos variables
$$\frac{d y}{y} = – Tan (x) dx$$
Paso 3: Integramos
$$\int \frac{d y}{y} = – \int Tan (x) dx + C$$
Desarrollando: $\int Tan (x) dx = \int \frac{sen (x)}{\cos (x)} dx$
$u = \cos (x)$
$d u = – sen (x) dx$
Entonces:
$\int \frac{d u}{u} = Ln u+C$
Por tanto:
$\int Tan (x) dx = \int \frac{sen (x)}{\cos (x)}dx = – Ln (\cos (x)) + C$
De modo que:
$$Ln (y) = – (- Ln (\cos (x)) + C)$$
$$Ln (y) = Ln (\cos (x)) + C_{1}$$
Esto implica:
$$y (x) = e^{Ln (\cos (x)) + C_{1}}$$
Y por último:
$$y (x) = C_2 \cos (x)$$
Saludos
Hola quisiera por favor que me respondas xq no puedo hacer esta ecuación
(sen x)y’=cosx
Muchas gracias desde ya espero tu respuesta
Pamela, ahora me pongo a tu servicio para la solución de tus ecuaciones diferenciales en el siguiente enlace:
Resuelvo cualquier ecuación diferencial, click aquí.
El servicio cuesta $5 USD y puedo resolverte hasta 1, 2 o hasta 3 ejercicios que me envies por medio de fiverr
De modo que estoy a tus ordenes.
Saludos
AVR
Hola, espero que me ayude, en esto : dy/dx = (2x-5y+3)/(2x-4y-6) , seria bueno si me la enviame a mi correo, que me lo pide aca abajo, espero que me responda
Diego, ahora me pongo a tu servicio para la solución de tus ecuaciones diferenciales en el siguiente enlace:
Resuelvo cualquier ecuación diferencial, click aquí.
El servicio cuesta $5 USD y puedo resolverte hasta 1, 2 o hasta 3 ejercicios que me envies por medio de fiverr
De modo que estoy a tus ordenes.
Saludos
AVR
excelente, usted es el mejor en la web
Gracias Josue por tu comentario. Es un gusto saber que te ha servido el blog. Te agredeceré muchísimo si me ayudas a difundirlo dandole un like a la pagina de facebook que te dejo en el siguiente enlace: Ecuaciones Diferenciales Ejercicios y Aplicaciones, click aquí
Saludos
hola tengo un problema con ecuaciones diferenciales por separación de variable
dy/dx=Xe con su exponente 6x-5y
Hola Ivonne
Podrías escribir las ED en una sola exhibition?
Es decir, por ejemplo, me parece que la ED que escribiste, en una sola exhibición, sería:
$\frac{dy}{dx}=xe^{6x-5y}$
Es correcto?
de otra forma podría ser:
$\frac{dy}{dx}=xe^{6x}-5y$
Es esta la correta?
Para señalar una variable «x» elevada a una exponente, puedes utilizar el simbolo «^», ok?
Agradezco tu aclaración
ocupo ayuda con esta ecuacion dy/dx= raiz cuadrada de tanx
Fran
Ahora ofrezco la solución de ejercicios de ecuaciones diferenciales mediante la compra de Gigs en fiverr.
Dale click al siguiente link: Yo resuelvo tus ecuaciones diferenciales, click auqí
Especialmente como la que me pides cuyo desarrollo es muy extenso.
Saludos
Amigo entendí completamente tu teoría. Pero quedé confundido cuando realizas las gráficas. ¿Cómo realizas estas gráficas? Si tengo una función determinada, como sacas las »familias» de las ecuaciones.
Puedes escribirme a mi correo: andresgranados06@gmail.com
Saludos desde Colombia.
Andrés
Las gráficas de las soluciones de cualquier ED se obtienen simplemente graficando la función solución como graficarías cualquier función solución.
Ahora:
1. Si la función solución es general, es decir, cuando no es una solución particular, entonces lo que obtienes es una famila de soluciones al otorgar valores diversos a las constantes de solución (como C1 o C2).
2. Si la función solución es particular entonces la gráfica de la solución solo es UNA curva solción.
Para graficar las funciones solución puedes dirigirte a esta página:
Haz tu simulación, click aquí
y leyendola podrás realizar tus propias gráficas en SAGE
Si aun no te queda claro te recomiendo comprar mi producto: Cómo entender y resolver una ecuación diferencial lineal en 4 pasos, click aquí
Un saludo
necesito ayuda con este ejercicio de segunda ley de newton y masa variable.
una cadena de 10 pies de largo esta enroyada holgadamente sobre el piso, un extremo de la cadena se jala verticalmente hacia ariiba con una fuerza constante de 5 libras, la cadena pesa 1lb/ft.
determine una ecuacion diferencial para el peso x(t) del extrmo localizado por encima del nivel del piso en el tiempo t.
asuma que la direccion positiva es ascendente
yensy
Enla compra de un gigg en fiverr siguiendo el siguiente enlace, fiverr, click aquí te resulvo tu problema.
Te agradezco de antemano y espero tu respuesta.
Saludos
ayuda porfavor
y(sqrt(x^2+y^2)) dx – x(x + sqrt(x^2+y^2)) dy = 0
Con gusto nicolás.
Comprandome un Gigg en fiverr, click aquí
Saludos
Tengo estos problemas si me puedes ayudar (3x^2 – 2xy + 3y^2)dx = 4xy dy y otro ( x^3+y^3)dx + 3x y^2=0
Que tal Winner
Con mucho gusto.
Tengo el servicio de solución de Ecuaciones Diferfenciales mediante el compro de un Gigg en la plataforma fiverr.
Acá te dejo el enlace: Resuelvo Cualquier Ecuación Diferencial, click aquí
Espero tu apoyo
Saludos
Hola profe…
He presentado dificultad con este ejercicio si tiene la posibilidad de ayudarme se lo agradeceria.
resuelve la siguiente ecuacion diferencial por el metodo de variable separadas.
e^(-y)+e^(-y)+e^(-2x-y)=e^x y dy/dx
Hola Juan
Con mucho gusto te ayudo
Tengo el servicio de solución de Ecuaciones Diferenciales mediante fiverr
Comprandome un Gigg con gusto te ayudo con tu ejercicio
te dejo el enlace a mi servicio en fiverr: Yo resuelvo tus problemas de Ecuaciones Diferenciales, click aquí
Espero tu respuesta
Saludos
porfavor ayudarme con este ejercicio dy/dx=x/x^2y+y^3… por el metodo de bernoulli….Gracias
Elier, te ayudo con mucho gusto
Tengo un servicio en fiverr para solución de ED’s
Te dejo el enlace: Yo voy a resolver tus problemas de ED’s, click aquí
Saludos
Elier
Con gusto , lo hago mediante fiverr
Tendrías que comprar un gigg
Buenas tardes, Hace poco descubrí esta página. Necesito que me ayude con este problema: xdx + ye^x dy = 0
Con mucho gusto Yeny.
Contratando mi servicio en fiverr.
Puedes encontrar un enlace en el margen izquierdo de la página.
hola mi nombre es fernanda me gustaría que me ayudaran con esta ecuación por variables separables la ecuación es y’=(2y+3/4x+5)
Hola fernanda
Una disculpa por no poder desarrollar tu respuesta.
Revisa en le relglón «# Ecuacion Diferencial», si he escrito la ED que me pides, si no, edita dicho renglón con la ED que me pides.
Saludos
me puedes ayudar con este problema
5xdy =1/x elevado a 3 dx
Jose
$5xdy=(\frac{1}{x})^{3}dx$
Solución:
Separación de variables
Paso-1: Forma estandar
$\frac{dy}{dx}=\frac{(\frac{1}{x})^{3}}{5x}$
$\frac{dy}{dx}=\frac{1}{5x^{4}}$
Paso-2: Separación Variables
$dy=\frac{1}{5x^{4}}dx$
Paso-3: Integración
$\int dy = \int \frac{1}{5x^{4}}dx$
Resolviendo y solución:
$y=-\frac{1}{15x^{3}} + C$
SAGE:
hola, no me sale este ejercicio
dm/dt= m-15
Caro, es una ED lineal
$\frac{dm}{dt}=m-15$
Es igual a:
$\frac{dm}{dt} – m = -15$
Es igual a:
$\frac{dm}{dt} – m = -15$
Lo puedes resolver con los pasos del siguiente artículo:
Ecuacion diferencial lineal ejercicios resueltos, click aquí
Saludos