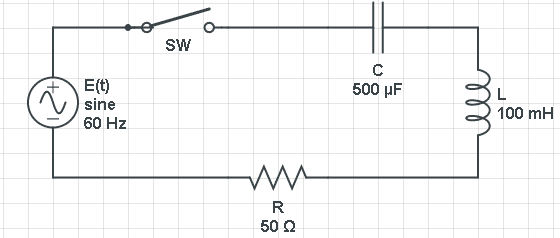
Aplicaciones Ecuaciones Diferenciales. Marcapasos de Corazón
Marcapasos de Corazón Si aprendes lo que te voy a enseñar en éste artículo sobre Aplicaciones Ecuaciones Diferenciales, conocerás una manera ordenada de Cómo ANALIZAR y MODELAR matemáticamente un Sistema Físico de Primer Orden, aplicando Ecuaciones Diferenciales Ordinarias Además, utilizarás el Método de Separación de Variables de 3 pasos propuesto en este sitio para simular un marcapaso […]
Aplicaciones Ecuaciones Diferenciales. Marcapasos de Corazón Leer más »